
【题目】袋中有7个球,其中4个白球,3个红球,从袋中任意取出2个球,求下列事件的概率:
(1) ![]() 取出的2个球都是白球;
取出的2个球都是白球;
(2)![]() 取出的2个球中1个是白球,另1个是红球.
取出的2个球中1个是白球,另1个是红球.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)用列举法可得从袋中7个球中一次任意取出2个球的基本事件的个数,其中取出的2个球均为白球的个数,再利用古典概型的概率计算公式即可得出;
(2)用列举法得到取出的2个球中1个是白球,另1个是红球基本事件个数,再利用古典概型的概率计算公式即可得.
设4个白球的编号为1,2,3,4,3个红球的编号为5,6,7,从袋中的7个小球中任取2个的方法为(1,2),(1,3),(1,4),(1,5),(1,6),(1,7) ,(2,3),(2,4),(2,5),(2,6),(2,7) ,(3,4),(3,5),(3,6),(3,7) ,(4,5),(4,6),(4,7) ,(5,6), (5,7) ,(6,7) ,共21种.
(1)从袋中的7个球中任取2个,所取的2个球全是白球的方法总数,即是从4个白球中任取2个的方法总数,共有6种,即为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).∴取出的2个球全是白球的概率为![]()
(2)从袋中的7个球中任取2个,其中1个为红球,而另1个为白球,其取法包括(1,5),(1,6),(1,7) ,(2,5),(2,6),(2,7) ,(3,5),(3,6),(3,7) ,(4,5),(4,6) ,(4,7) ,共12种.
∴取出的2个球中1个是白球,另1个是红球的概率为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知点![]() 在椭圆
在椭圆![]() 上,将射线
上,将射线![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() ,所得射线
,所得射线![]() 交直线
交直线![]() 于点
于点![]() .以
.以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求椭圆![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)证明::![]() 中,斜边
中,斜边![]() 上的高
上的高![]() 为定值,并求该定值.
为定值,并求该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华中师大附中中科教处为了研究高一学生对物理和数学的学习是否与性别有关,从高一年级抽取60,名同学(男同学30名,女同学30名),给所有同学物理题和数学题各一题,让每位同学自由选择一道题进行解答.选题情况如下表:(单位:人)

(1)在犯错误的概率不超过1%是条件下,能否判断高一学生对物理和数学的学习与性别有关?
(2)经过多次测试后发现,甲每次解答一道物理题所用的时间5—8分钟,乙每次解答一道物理题所用的时间为6—8分钟,现甲、乙解同一道物理题,求甲比乙先解答完的概率;
(3)现从选择做物理题的8名女生中任意选取两人,对题目的解答情况进行全程研究,记甲、乙两女生被抽到的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的焦点弦的弦长为
轴的焦点弦的弦长为![]() ,过
,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,
,![]() 互相垂直,直线
互相垂直,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于点
交于点![]() ,
,![]() 两点,直线
两点,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点.求
两点.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极值;
的极值;
(Ⅱ)若函数![]() 的两个零点为
的两个零点为![]() ,记
,记![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)极大值为![]() ,无极小值;(Ⅱ)证明见解析.
,无极小值;(Ⅱ)证明见解析.
【解析】分析:(Ⅰ)先判断函数![]() 在
在![]() 上的单调性,然后可得当
上的单调性,然后可得当![]() 时,
时,![]() 有极大值,无极小值.(Ⅱ)不妨设
有极大值,无极小值.(Ⅱ)不妨设![]() ,由题意可得
,由题意可得![]() ,即
,即![]() ,又由条件得
,又由条件得![]() ,构造
,构造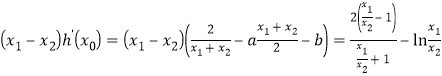 ,令
,令![]() ,则
,则![]() ,利用导数可得
,利用导数可得![]() ,故得
,故得![]() ,又
,又![]() ,所以
,所以![]() .
.
详解:(Ⅰ)![]() ,
,
![]() ,
,
由![]() 得
得![]() ,
,
且当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递减,
上单调递减,
∴当![]() 时,
时,![]() 有极大值,且
有极大值,且![]() ,无极小值.
,无极小值.
(Ⅱ)![]() 函数
函数![]() 的两个零点为
的两个零点为![]() ,不妨设
,不妨设![]() ,
,
![]() ,
,![]() .
.
![]()
![]() ,
,
即![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,

![]()
![]()
 .
.
令![]() ,则
,则![]()
![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
故![]() ,
,
 ,
,
即![]() ,
,
又![]() ,
,
![]() .
.
点睛:(1)研究方程根的情况,可以通过导数研究函数的单调性、最大(小)值、函数的变化趋势等,根据题目要求,画出函数图象的大体图象,然后通过数形结合的思想去分析问题,可以使得问题的求解有一个清晰、直观的整体展现.
(2)证明不等式时常采取构造函数的方法,然后通过判断函数的单调性,借助函数的最值进行证明.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点
).以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com