
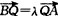 ,经过点Q与x轴垂直的直线交抛物线于点M,点P满足
,经过点Q与x轴垂直的直线交抛物线于点M,点P满足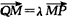 ,求点P的轨迹方程。
,求点P的轨迹方程。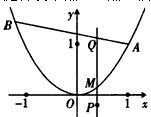
解:由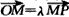 知Q,M,P三点在同一条垂直于x轴的直线上,
知Q,M,P三点在同一条垂直于x轴的直线上,
故可设P(x,y),Q(x,y0),M(x,x2),
则x2-y0=λ(y-x2),
即y0=(1+λ)x2-λy ①
再设B(x1,y1),由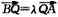
即(x-x1,y0-y1)=λ(1-x,1-y0),
解得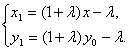 ②
②
将①式代入②式,消去y0,
得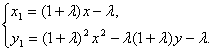 ③
③
又点B在抛物线y=x2上,所以y1=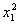 ,再将③式代入y1=
,再将③式代入y1=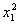
得(1+λ)2x2-λ(1+λ)y-λ=((1+λ)x-λ)2,
(1+λ)2x2-λ(1+)y-λ=(1+λ)2x2-2λ(1+λ)x+λ2,
2(1+λ)x-λ(1+λ)y-λ(1+λ)=0
因λ>0,两边同除以λ(1+λ),得2x-y-1=0
故所求点P的轨迹方程y=2x-1。


科目:高中数学 来源: 题型:
设函数![]() (x)=
(x)=![]() ,g(x)=ax2+bx
,g(x)=ax2+bx![]() 若y=f(x)的图像与y=g(x)图像有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是
若y=f(x)的图像与y=g(x)图像有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是
A.当a<0时,x1+x2<0,y1+y2>0
B. 当a<0时, x1+x2>0, y1+y2<0
C.当a>0时,x1+x2<0, y1+y2<0
D. 当a>0时,x1+x2>0, y1+y2>0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷(解析版) 题型:解答题
设椭圆C: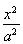 +
+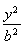 =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为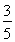 .
.
(1)求C的方程;
(2)求过点(3,0)且斜率为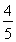 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
椭圆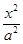 +
+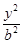 =1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=
=1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=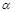 , 且
, 且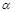 ∈[
∈[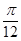 ,
,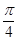 ], 则该椭圆离心率的取值范围为 (
)
], 则该椭圆离心率的取值范围为 (
)
A.[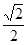 ,1 ) B.[
,1 ) B.[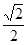 ,
,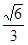 ] C.[
] C.[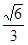 , 1) D.[
, 1) D.[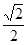 ,
,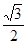
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三第五次质量检测理科数学 题型:选择题
.椭圆 +
+ =1(a>b>0)上一点A关于原点的对称点为B,F为其右焦点,若AF⊥BF,设∠ABF=
=1(a>b>0)上一点A关于原点的对称点为B,F为其右焦点,若AF⊥BF,设∠ABF= ,且
,且 ∈[
∈[ ,
, ],则该椭圆离心率的取值范围为
],则该椭圆离心率的取值范围为
A.[ ,1 ) B.[
,1 ) B.[ ,
, ]
]
C.[ ,1) D.[
,1) D.[ ,
, ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com