
【题目】如图,已知四棱锥S﹣ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点. 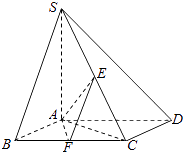
(1)证明:SD⊥AF;
(2)若AB=2,SA=4,求二面角F﹣AE﹣C的余弦值.
【答案】
(1)证明:由四边形ABCD为菱形,∠ADC=60°,可得△ABC为正三角形.
因为F为BC的中点,所以AF⊥BC.
又BC∥AD,因此AE⊥AD.
因为SA⊥平面ACDB,AE平面ABCD,所以SA⊥AF.
而SA平面SAD,AD平面SAD且SA∩AD=A,
所以AF⊥平面PAD.又SD平面SAD,
所以AF⊥SD.
(2)解:由(1)知AF,AD,AS两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E,F分别为SC,BC的中点,所以 ![]() ,
, ![]() ,
,
所以 ![]() .
.
设平面AEF的一法向量为 ![]() ,
,
则 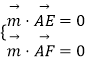 因此
因此 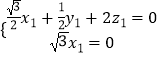
取Z1=﹣1,则 ![]() ,
,
因为BD⊥AC,BD⊥SA,SA∩AC=A,
所以BD⊥平面AEC,
故 ![]() 为平面AEC的一法向量,且
为平面AEC的一法向量,且 ![]() ,
,
所以 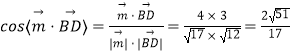 ,
,
由于二面角E﹣AF﹣C为锐角,所以所求二面角的余弦值为 ![]() .
.
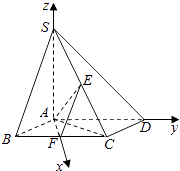
【解析】(1)证明AF⊥BC.SA⊥AF.推出AF⊥平面PAD.然后利用直线与平面垂直的性质定理证明AF⊥SD.(2)以A为坐标原点,建立如图所示的空间直角坐标系,求出相关点的坐标,求出平面AEF的一法向量,平面AEC的一法向量,通过斜率的数量积求解二面角的余弦值即可.
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识,掌握垂直于同一个平面的两条直线平行.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】已知点F(0,1),直线l:y=﹣1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且 ![]() .
.
(1)求动点P的轨迹C的方程;
(2)已知圆M过定点D(0,2),圆心M在轨迹C上运动,且圆M与x轴交于A、B两点,设|DA|=l1 , |DB|=l2 , 求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为![]() ,
, ![]() ,…,
,…, ![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
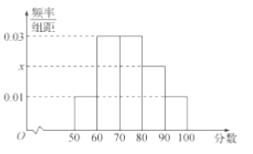
(1)求频率分布直方图中的![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若在样本中,利用分层抽样的方法从成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求![]() 两组中至少有1人被抽到的概率.
两组中至少有1人被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系p= ![]()
该商品的日销售量Q(件)时间t(天)的函数关系Q=﹣t+40(0<t≤30,t∈N*)
求该商品的日销售额的最大值,并指出日销售额最大一天是30天中的第几天?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一 、高二 、高三三个年级共有 ![]() 名教师,为调查他们的备课时间情况,通过分层
名教师,为调查他们的备课时间情况,通过分层
抽样获得了![]() 名教师一周的备课时间 ,数据如下表(单位 :小时):
名教师一周的备课时间 ,数据如下表(单位 :小时):
高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
(1)试估计该校高三年级的教师人数 ;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲 ,高二年级选出的人记为乙 ,求该周甲的备课时间不比乙的备课时间长的概率 ;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是![]() (单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为![]() ,表格中的数据平均数记为
,表格中的数据平均数记为![]() ,试判断
,试判断![]() 与
与![]() 的大小. (结论不要求证明)
的大小. (结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com