
【题目】椭圆![]() (a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(1)求椭圆的方程;
(2)直线l:y=kx+m与椭圆交于点A,C,线段AC的中点为M,射线MO与椭圆交于点P,点O为△PAC的重心,求证:△PAC的面积S为定值;
【答案】(1)![]() 1;(2)见解析
1;(2)见解析
【解析】
(1)由题意得b=c,BF1=2,求出a、b后即可得解;
(2)设A(x1,y1),B(x2,y2),P(x0,y0),联立方程组得![]() ,
,![]() ,由题意x0
,由题意x0![]() ,y0
,y0![]() ,△PAC的面积
,△PAC的面积![]()
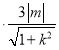 ,化简即可得证.
,化简即可得证.
(1)根据题意,由△BF1F2为等腰直角三角形可得b=c,
直线BF1:y=x+b被圆x2+y2=b2所截得的弦长为2,即BF1=2,
所以a=2,![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() 1;
1;
(2)证明:直线l的方程为y=kx+m,设A(x1,y1),B(x2,y2),
联立![]() ,可得(1+2k2)x2+4kmx+2m2﹣4=0,
,可得(1+2k2)x2+4kmx+2m2﹣4=0,
x1+x2![]() ,x1x2
,x1x2![]() ,y1+y2=k(x1+x2)+2m
,y1+y2=k(x1+x2)+2m![]() ,
,
由题意点O为△PAC重心,设P(x0,y0),可得![]() 0,
0,![]() 0,
0,
所以x0=-(x1+x2)![]() ,y0=-(y1+y2)
,y0=-(y1+y2)![]() ,
,
代入椭圆![]() 1;得
1;得![]() 1,化为2m2=1+2k2,
1,化为2m2=1+2k2,
设坐标原点O到直线l的距离为d,
则△PAC的面积S![]() |AC|3d
|AC|3d![]() |x1﹣x2|
|x1﹣x2|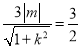 |m||x1﹣x2|
|m||x1﹣x2|![]() |m|
|m|
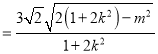 |m|=3
|m|=3![]()
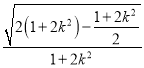
![]() .
.
可得△PAC的面积S为定值![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 是定义为R的偶函数,且
是定义为R的偶函数,且![]() 对任意的
对任意的![]() ,都有
,都有![]() 且当
且当![]() 时,
时, ![]() ,若在区间
,若在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰好有3个不同的实数根,则
恰好有3个不同的实数根,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年双11当天,某购物平台的销售业绩高达2135亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系,现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.9,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为140次.
(1)请完成下表,并判断是否可以在犯错误概率不超过0.5%的前提下,认为商品好评与服务好评有关?
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 | 140 | ||
对商品不满意 | 10 | ||
合计 | 200 |
(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全好评的次数为X.
①求随机变量X的分布列;
②求X的数学期望和方差.
附:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上任意一点
上任意一点![]() 满足
满足![]() ,直线
,直线![]() 的方程为
的方程为![]() ,且与曲线
,且与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设点![]() ,直线
,直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?若过定点,求该定点的坐标.
是否过定点?若过定点,求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ABE﹣DCF和一个四棱锥P﹣ABCD组合而成,其中EF=EA=EB=2,AE⊥EB,PA=PD![]() ,平面PAD∥平面EBCF.
,平面PAD∥平面EBCF.
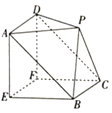
(1)证明:平面PBC∥平面AEFD;
(2)求直线AP与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件,为激发大家的学习兴趣,他们推出了“解数学题获取软件激活码”的活动,这款软件的激活码为下列数学问题的答案:已知数列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,……,以此类推,求满足如下条件的最小整数
,……,以此类推,求满足如下条件的最小整数![]() 且该数列的前
且该数列的前![]() 项和为2的整数幂,那么该软件的激活码是________。
项和为2的整数幂,那么该软件的激活码是________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com