
【题目】如图,在多面体![]() 中,
中, ![]() 平面
平面![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为30°,
所成的角为30°,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.

【答案】(1)见解析(2)60°
【解析】分析:
(Ⅰ)由BD⊥平面ABC得BD⊥AC,上AC⊥AB,得AC⊥平面ABDE,从而知∠CDA是直线CD与平面ABDE所成的角为30°,这样可求得AC与BC的关系从而确定![]() 是等腰直角三角形,于是取BC中点为O,有AO⊥BC,因此可证AO⊥平面CBD,又可证AOME是平行四边形,即得AO//EM,于是有EM⊥平面BCD,最终可证得面面垂直;
是等腰直角三角形,于是取BC中点为O,有AO⊥BC,因此可证AO⊥平面CBD,又可证AOME是平行四边形,即得AO//EM,于是有EM⊥平面BCD,最终可证得面面垂直;
(Ⅱ) 以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() 如图所示,不妨设
如图所示,不妨设![]() ,写出各点坐标,然后求出平面BCE和平面BEM的法向量,利用向量法可求得二面角.
,写出各点坐标,然后求出平面BCE和平面BEM的法向量,利用向量法可求得二面角.
详解:
(Ⅰ)连接![]() ,取
,取![]() 的中点为
的中点为![]() ,连接
,连接![]() .
.
因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
则![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() .
.
所以![]() ,
,
所以![]() 是等腰直角三角形,则
是等腰直角三角形,则![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]()
![]()
![]() 又
又![]() ,所以
,所以![]()
![]()
![]() ,
,
故四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅱ)以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() 如图所示,不妨设
如图所示,不妨设![]() ,
,
则 ,
,
所以 .
.
设平面 ![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即 ,解得
,解得 ,
,
令![]() ,得
,得![]() ;
;
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即 ,解得
,解得 ,
,
令![]() ,得
,得![]() ;
;
所以![]() ,
,
所以二面角![]() 的大小为60°.
的大小为60°.


科目:高中数学 来源: 题型:
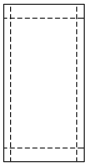
【题目】学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128 dm2,上、下两边各空2 dm,左、右两边各空1 dm.如何设计海报的尺寸,才能使四周空白面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 中点.将
中点.将![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图2).
(如图2).

(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出
? 若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点.将
中点.将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置, 使
的位置, 使![]() 如图2.
如图2.
(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)设![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点,试比较三棱锥
的中点,试比较三棱锥![]() 和三棱锥
和三棱锥![]() (图中未画出)的体积大小,并说明理由.
(图中未画出)的体积大小,并说明理由.

图1 图2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() ,
,![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求曲线![]() 上的点到曲线
上的点到曲线![]() 的距离的最大值和最小值.
的距离的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)对任意的m,n∈R都有f(m+n)=f(m)+f(n)-1,并且x>0时,恒有f(x)>1.
(1)求证:f(x)在R上是增函数;
(2)若f(3)=4,解不等式f(a2+a-5)<2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :
: ![]() 表示双曲线,命题
表示双曲线,命题![]() :
: ![]() 表示椭圆。
表示椭圆。
(1)若命题![]() 与命题
与命题![]() 都为真命题,则
都为真命题,则![]() 是
是![]() 的什么条件?
的什么条件?
(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个)
(2)若![]() 为假命题,且
为假命题,且![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com