
| ax2+1 |
| bx+c |
| 5 |
| 2 |
| ax2+1 |
| bx+c |
| ax2+1 |
| -bx+c |
| ax2+1 |
| bx+c |
| ax |
| b |
| 1 |
| bx |
|
|
| ax |
| b |
| 1 |
| bx |
| 1 | ||
|
| 1 |
| bx |
| 1 |
| b |
| 5 |
| 2 |
| 1 |
| 2 |
| x2+1 |
| x |
|
|
|
|
|
| 2 |
| 2 |
| 2 |
| 2 |


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
 |
| y |
| A、若该大学某女生身高为170cm,则可断定其体重必为58.79kg | ||||
B、回归直线过样本点的中心(
| ||||
| C、若该大学某女生身高增加1cm,则其体重约增加0.85kg | ||||
| D、y与x具有正的线性相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:
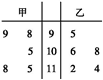 在某中学举行的跳高比赛选拨赛中,甲和乙进行了5次比赛,他们的成绩用如图所示的茎叶图表示,则下列说法正确的是( )
在某中学举行的跳高比赛选拨赛中,甲和乙进行了5次比赛,他们的成绩用如图所示的茎叶图表示,则下列说法正确的是( )| A、甲的平均成绩比乙的平均成绩高,甲比乙成绩稳定 |
| B、甲的平均成绩比乙的平均成绩低,乙比甲成绩稳定 |
| C、甲的平均成绩与乙的平均成绩一样,但甲比乙成绩稳定 |
| D、甲的平均成绩与乙的平均成绩一样,但乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、34种 | B、35种 |
| C、120种 | D、140种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com