【题目】为了调查某社区中学生的课外活动，对该社区的100名中学生进行了调研，随机抽取了若干名，年龄全部介于13与18之间，将年龄按如下方式分成五组:第一组
；第二组
；第五组
.按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前三个组的频率之比为
，且第二组的频数为4.
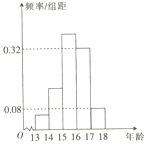
（1）试估计这100名中学生中年龄在
内的人数；
（2）求调研中随机抽取的人数.
科目：高中数学 来源： 题型：
【题目】 在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东
且与点A相距40
海里的位置B，经过40分钟又测得该船已行驶到点A北偏东+
(其中sin=
，
)且与点A相距10
海里的位置C.
（I）求该船的行驶速度（单位：海里/小时）;
（II）若该船不改变航行方向继续行驶.判断它是否会进入警戒水域，并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的各项均为正数，a1=1，前n项和为Sn ， 且an+12﹣nλ2﹣1=2λSn ， λ为正常数．
（1）求数列{an}的通项公式；
（2）记bn= 
，Cn= 
+ 
（k，n∈N*，k≥2n+2）． 求证：
①bn＜bn+1；
②Cn＞Cn+1 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设a ， b ， c是正整数，且a∈[70，80），b∈[80，90），c∈[90，100]，当数据a ， b ， c的方差最小时，a+b+c的值为( )
A.252或253
B.253或254
C.254或255
D.267或268
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱柱ABCD﹣A1B1C1D1中，底面ABCD为菱形，AA1⊥底面ABCD，E为B1D的中点．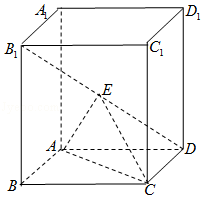 
（Ⅰ）证明：平面ACE⊥平面ABCD；
（Ⅱ）若二面角D﹣AE﹣C为60°，AA1=AB=1，求三棱锥C﹣AED的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若函数
满足：在定义域
内存在实数
，使得
成立，则称函数
为“
的饱和函数”.给出下列四个函数：①
；②
； ③
；④
.其中是“
的饱和函数”的所有函数的序号是______________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）在R上存在导数f′（x），x∈R，有f（﹣x）+f（x）=x2 ， 在（0，+∞）上f′（x）＜x，若f（6﹣m）﹣f（m）﹣18+6m≥0，则实数m的取值范围为（ ）
A.[﹣3，3]
B.[3，+∞）
C.[2，+∞）
D.（﹣∞，﹣2]∪[2，+∞）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线l的参数方程为 
（t为参数），曲线C的极坐标方程是 
以极点为原点，极轴为x轴正方向建立直角坐标系，点M（﹣1，0），直线l与曲线C交于A，B两点．
（1）写出直线l的极坐标方程与曲线C的普通方程；
（2）线段MA，MB长度分别记|MA|，|MB|，求|MA||MB|的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
