
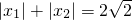 ,求b的最大值;
,求b的最大值; 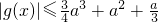 .
.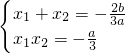
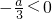
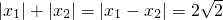
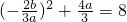
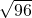 =
=
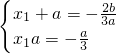 ?
?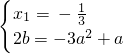
 )
) a=(x+
a=(x+ )(3ax-3a2-a)
)(3ax-3a2-a) 对称
对称 和
和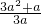 ,且-
,且- <
<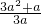
 ,a),a
,a),a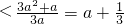
 )=
)=
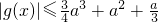 恒成立.
恒成立.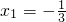 ,且2b-3a2+a.由此代入g(x)=f(x)'-a(x-
,且2b-3a2+a.由此代入g(x)=f(x)'-a(x- 和
和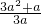 ,且-
,且- <
<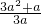 .因为x1<x<x2,所以g(x)的定义域为∈(-
.因为x1<x<x2,所以g(x)的定义域为∈(- ,a)?(-
,a)?(- ,
,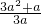 ),得到g(x)的值恒为负数.并且g(x)的最小值等于二次函数对称轴处的取值:g(
),得到g(x)的值恒为负数.并且g(x)的最小值等于二次函数对称轴处的取值:g( )=
)= ,从而证出原不等式恒成立.
,从而证出原不等式恒成立.

 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
| a | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x1)-f(x2) |
| x1-x2 |
| f(x1)-f(x2) |
| x1-x2 |
查看答案和解析>>
科目:高中数学 来源:广东省2007年五校联考调研数学试卷(理科)-苏教版 题型:044
设x1,x2是![]() 的两个极值点,f(x)的导函数是
的两个极值点,f(x)的导函数是![]()
(1)如果x1<2<x2<4,求证:![]() ;
;
(2)如果|x1|<2,|x2-x1|=2,求b的取值范围;
(3)如果a≥2,且x2-x1=2,x∈(x1,x2)时,函数![]() 的最小值为h(a),求h(a)的最大值.
的最小值为h(a),求h(a)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
①f(x1)f(-x1)≤0 ②f(x2)f(-x2)>0 ③f(x1)+f(x2)≤f(-x1)+f(-x2)④f(x1)+f(x2)≥f(-x1)+f(-x2)
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| f(x1)-f(x2) |
| x1-x2 |
| f(x1)-f(x2) |
| x1-x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com