练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点，且EH∥FG．求证：EH∥BD．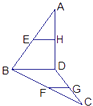

    【答案】证明：∵EH∥FG，EH面BCD，FG面BCD ∴EH∥面BCD，
    又∵EH面ABD，面BCD∩面ABD=BD，
    ∴EH∥BD
    【解析】先由EH∥FG，得到EH∥面BDC，从而得到EH∥BD．
    【考点精析】关于本题考查的空间中直线与直线之间的位置关系和直线与平面平行的判定，需要了解相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点；平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】定义在R上的偶函数f（x）满足f（x+1）= ，且f（x）在[﹣3，﹣2]上是减函数，若α，β是锐角三角形的两个内角，则（ ）
    A.f（sinα）＞f（sinβ）
    B.f（cosα）＞f（cosβ）
    C.f（sinα）＞f（cosβ）
    D.f（sinα）＜f（cosβ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于实数a和b，定义运算“*”： ，设f（x）=（2x﹣1）*（x﹣1），且关于x的方程为f（x）=m（m∈R）恰有三个互不相等的实数根x1 ， x2 ， x3 ， 则实数m的取值范围是；x1+x2+x3的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a∈R，函数f（x）=（﹣x2+ax）ex ， （x∈R，e为自然对数的底数）
    （1）当a=2时，求函数f（x）的单调递增区间．
    （2）函数f（x）是否为R上的单调函数，若是，求出a的取值范围；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】观察以下三个等式： sin215°﹣sin245°+sin15°cos45°=﹣ ，
    sin220°﹣sin250°+sin20°cos50°=﹣ ，
    sin230°﹣sin260°+sin30°cos60°=﹣ ；
    猜想出一个反映一般规律的等式： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图：在四棱锥V﹣ABCD中，底面ABCD是边长为2的正方形，其它四个侧面都是侧棱长为 的等腰三角形．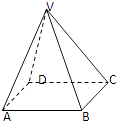
    （1）求二面角V﹣AB﹣C的平面角的大小；
    （2）求四棱锥V﹣ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对正整数n，设曲线y=xn（1﹣x）在x=2处的切线与y轴交点的纵坐标为an ， 则数列 的前n项和的公式是（ ）
    A.2n
    B.2n﹣2
    C.2n+1
    D.2n+1﹣2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= x2+2ax，g（x）=3a2lnx+b，设两曲线y=f（x），y=g（x）有公共点，且在该点处的切线相同，则a∈（0，+∞）时，实数b的最大值是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】放射性元素由于不断有原子放射出微粒子而变成其他元素，其含量不断减少，这种现象称为衰变．假设在放射性同位素铯137的衰变过程中，其含量M（单位：太贝克）与时间t（单位：年）满足函数关系：M（t）=M0 ，其中M0为t=0时铯137的含量．已知t=30时，铯137含量的变化率是﹣10In2（太贝克/年），则M（60）=（ ）
    A.5太贝克
    B.75In2太贝克
    C.150In2太贝克
    D.150太贝克

    查看答案和解析>>

    同步练习册答案