
【题目】经市场调查,某超市的一种商品在过去的一个月内(以30天计算),销售价格![]() 与时间(天)的函数关系近似满足
与时间(天)的函数关系近似满足![]() ,销售量
,销售量![]() 与时间(天)的函数关系近似满足
与时间(天)的函数关系近似满足 .
.
(1)试写出该商品日销售金额![]() 关于时间
关于时间![]() 的函数表达式;
的函数表达式;
(2)求该商品的日销售金额![]() 的最大值与最小值.
的最大值与最小值.
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】为了研究某种微生物的生长规律,研究小组在实验室对该种微生物进行培育实验.前三天观测的该微生物的群落单位数量分别为12,16,24.根据实验数据,用y表示第![]() 天的群落单位数量,某研究员提出了两种函数模型;①
天的群落单位数量,某研究员提出了两种函数模型;①![]() ;②
;②![]() ,其中a,b,c,p,q,r都是常数.
,其中a,b,c,p,q,r都是常数.
(1)根据实验数据,分别求出这两种函数模型的解析式;
(2)若第4天和第5天观测的群落单位数量分别为40和72,请从这两个函数模型中选出更合适的一个,并计算从第几天开始该微生物群落的单位数量超过1000.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为平面直角坐标系
的顶点为平面直角坐标系![]() 的坐标原点
的坐标原点![]() ,焦点为圆
,焦点为圆![]() 的圆心
的圆心![]() .经过点
.经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点,
两点,![]() 在第一象限,
在第一象限,![]() 在第四象限.
在第四象限.
(1)求抛物线![]() 的方程;
的方程;
(2)是否存在直线![]() 使
使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,AB=2AD,
中,AB=2AD,![]() 为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
为DC的中点,将△ADM沿AM折起使平面ADM⊥平面ABCM.
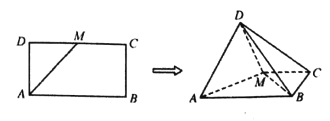
(1)当AB=2时,求三棱锥![]() 的体积;
的体积;
(2)求证:BM⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为实数,数列
为实数,数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)当![]() 和
和![]() 时,分别写出数列
时,分别写出数列![]() 的前5项;
的前5项;
(Ⅱ)证明:当![]() 时,存在正整数
时,存在正整数![]() ,使得
,使得![]() ;
;
(Ⅲ)当![]() 时,是否存在实数
时,是否存在实数![]() 及正整数
及正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ?若存在,求出实数
?若存在,求出实数![]() 及正整数
及正整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中![]() 中,直线
中,直线![]() ,圆
,圆![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.


(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,且
的左、右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上任意一点,以
为椭圆上任意一点,以![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() ,当圆
,当圆![]() 与直线
与直线![]() :
:![]() 有公共点时,求
有公共点时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
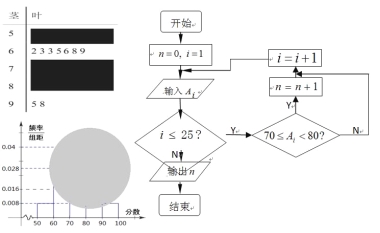
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com