
【题目】如图所示的多面体是由一个直平行六面体被平面![]() 所截后得到的,其中
所截后得到的,其中![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且椭圆的长轴长为4.
的离心率互为倒数,且椭圆的长轴长为4.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() (
(![]() )为椭圆
)为椭圆![]() 上一点,求
上一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的图像在点M(-1,f(-1))处的切线方程为x+2y+5=0,
的图像在点M(-1,f(-1))处的切线方程为x+2y+5=0,
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 经过点
经过点 ,左右焦点分别为
,左右焦点分别为![]() 、
、![]() ,圆
,圆![]() 与直线
与直线![]() 相交所得弦长为2.
相交所得弦长为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上不在
上不在![]() 轴上的一个动点,
轴上的一个动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两个不同的点.
两个不同的点.
(1)试探究![]() 的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
(2)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 经过点
经过点 ,左右焦点分别为
,左右焦点分别为![]() 、
、![]() ,圆
,圆![]() 与直线
与直线![]() 相交所得弦长为2.
相交所得弦长为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上不在
上不在![]() 轴上的一个动点,
轴上的一个动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两个不同的点,求
两个不同的点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车从![]() 市出发沿海岸一条笔直公路以每小时
市出发沿海岸一条笔直公路以每小时![]() 的速度向东均速行驶,汽车开动时,在
的速度向东均速行驶,汽车开动时,在![]() 市南偏东方向距
市南偏东方向距![]() 市
市![]() 且与海岸距离为
且与海岸距离为![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?
(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与![]() 所成的角.
所成的角.

查看答案和解析>>
科目:高中数学 来源: 题型:
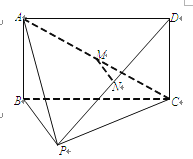
【题目】如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M为AC的中点,N为PD上一点.
(1)若MN∥平面ABP,求证:N为PD的中点;
(2)若平面ABP⊥平面APC,求证:PC⊥平面ABP.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若点(p,q),在|p|≤3,|q|≤3中按均匀分布出现.
(1)点M(x,y)横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点M(x,y)落在上述区域的概率?
(2)试求方程x2+2px﹣q2+1=0有两个实数根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com