
【题目】如图,在正方体![]() 中,E,F,M,N分别是
中,E,F,M,N分别是![]() ,BC,
,BC,![]() ,
,![]() 的中点.
的中点.

(1)求证:平面![]() 平面NEF;
平面NEF;
(2)求二面角![]() 的平面角的正切值.
的平面角的正切值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量(单位:克)分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中,经统计得频率分布直方图如图所示.
中,经统计得频率分布直方图如图所示.
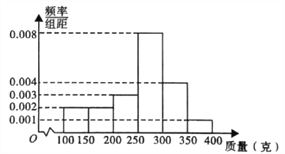
(1)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在
的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中恰有1个在![]() 内的概率;
内的概率;
(2)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出如下两种收购方案:
![]() 方案:所有芒果以10元/千克收购;
方案:所有芒果以10元/千克收购;
![]() 方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.
方案:对质量低于250克的芒果以2元/个收购,高于或等于250克的以3元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的首项
的首项![]() ,前n项和
,前n项和![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是公比为4的等比数列,且
是公比为4的等比数列,且![]() ,
,![]() ,
,![]() 也是等比数列,若数列
也是等比数列,若数列![]() 单调递增,求实数
单调递增,求实数![]() 的取值范围;
的取值范围;
(3)若数列![]() 、
、![]() 都是等比数列,且满足
都是等比数列,且满足![]() ,试证明: 数列
,试证明: 数列![]() 中只存在三项.
中只存在三项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国是世界互联网服务应用最好的国家,一部智能手机就可以跑遍国内所有地方,中国市场的移动支付普及率高得惊人.一家大型超市委托某高中数学兴趣小组调查该超市的顾客使用移动支付的情况,调查人员从年龄在![]() 内的顾客中,随机抽取了
内的顾客中,随机抽取了![]() 人,调查他们是否使用移动支付,结果如下表:
人,调查他们是否使用移动支付,结果如下表:
年龄 |
|
|
|
|
|
|
|
|
使用 |
|
|
|
|
|
|
|
|
不使用 |
|
|
|
|
|
|
|
|
(1)为更进一步推动移动支付,超市准备对使用移动支付的每位顾客赠送![]() 个环保购物袋,若某日该超市预计有
个环保购物袋,若某日该超市预计有![]() 人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为使用移动支付与年龄有关?
的把握认为使用移动支付与年龄有关?
年龄 | 年龄 | 小计 | |
使用移动支付 | |||
不使用移动支付 | |||
合计 |
附:下面的临界值表供参考:
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
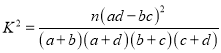 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD>BC.E,F分别为棱AB,PC上的点.

(1)求证:平面AFD⊥平面PAB;
(2)若点E满足![]() ,当F满足什么条件时,EF∥平面PAD?请给出证明.
,当F满足什么条件时,EF∥平面PAD?请给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成的角为60°.

(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 ,(为参数),曲线C的参数方程为
,(为参数),曲线C的参数方程为 (α为参数).
(α为参数).
(Ⅰ)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(3,![]() ),判断点P与直线l位置关系;
),判断点P与直线l位置关系;
(Ⅱ)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com