
【题目】已知定义在(0, ![]() )上的函数f(x)的导函数为f′(x),且对于任意的x∈(0,
)上的函数f(x)的导函数为f′(x),且对于任意的x∈(0, ![]() ),都有f′(x)sinx<f(x)cosx,则( )
),都有f′(x)sinx<f(x)cosx,则( )
A.![]() f(
f( ![]() )>
)> ![]() f(
f( ![]() )
)
B.f( ![]() )>f(1)
)>f(1)
C.![]() f(
f( ![]() )<f(
)<f( ![]() )
)
D.![]() f(
f( ![]() )<f(
)<f( ![]() )
)
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对于一切实数x,y均有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0,则当x∈(0, ![]() ),不等式f(x)+2<logax恒成立时,实数a的取值范围是
),不等式f(x)+2<logax恒成立时,实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为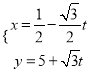 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)射线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是某地搜集到的新房屋的销售价格![]() 和房屋的面积
和房屋的面积![]() 的数据:
的数据:
房屋面积( | 115 | 110 | 80 | 135 | 105 |
销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为150![]() 时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
时的销售价格.附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,能推断这个几何体可能是三棱台的是( ) 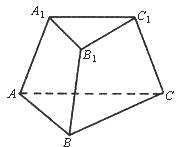
A.A1B1=2,AB=3,B1C1=3,BC=4
B.A1Bl=1,AB=2,BlCl=1.5,BC=3,A1C1=2,AC=3
C.AlBl=1,AB=2,B1Cl=1.5,BC=3,AlCl=2,AC=4
D.AB=A1B1 , BC=B1C1 , CA=C1A1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是( )
A.(x-2)2+(y-1)2=1
B.(x-2)2+(y-3)2=1
C.(x-3)2+(y-2)2=1
D.(x-3)2+(y-1)2=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com