
【题目】甲乙两名运动员互不影响地进行四次设计训练,根据以往的数据统计,他们设计成绩均不低于8环(成绩环数以整数计),且甲乙射击成绩(环数)的分布列如下:
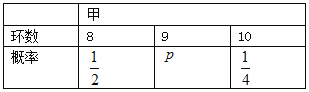
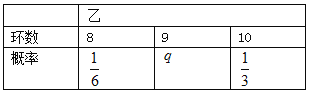
(I)求![]() ,
, ![]() 的值;
的值;
(II)若甲乙两射手各射击两次,求四次射击中恰有三次命中9环的概率;
(III)若两个射手各射击1次,记两人所得环数的差的绝对值为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的为________(正确序号全部填上)
(1)空间中,一个角的两边与另一个角的两边分别平行,则这两个角相等或互补;
(2)一个二面角的两个半平面与另一个二面角的两个半平面分别垂直,则这两个二面角相等或互补;
(3)直线![]() ,
,![]() 为异面直线,所成角的大小为
为异面直线,所成角的大小为![]() ,过空间一点
,过空间一点![]() 作直线
作直线![]() ,使l与直线
,使l与直线![]() 及直线
及直线![]() 都成相等的角
都成相等的角![]() ,这样的直线可作3条;
,这样的直线可作3条;
(4)直线![]() 与平面
与平面![]() 相交,过直线
相交,过直线![]() 可作唯一的平面与平面
可作唯一的平面与平面![]() 垂直.
垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,在《我是演说家》第四季这档节目中,英国华威大学留学生游斯彬的“数学之美”的演讲视频在微信朋友圈不断被转发,他的视角独特,语言幽默,给观众留下了深刻的印象.某机构为了了解观众对该演讲的喜爱程度,随机调查了观看了该演讲的140名观众,得到如下的列联表:(单位:名)
男 | 女 | 总计 | |
喜爱 | 40 | 60 | 100 |
不喜爱 | 20 | 20 | 40 |
总计 | 60 | 80 | 140 |
(1)根据以上列联表,问能否在犯错误的概率不超过0.05的前提下认为观众性别与喜爱该演讲有关.(精确到0.001)
(2)从这60名男观众中按对该演讲是否喜爱采取分层抽样,抽取一个容量为6的样本,然后随机选取两名作跟踪调查,求选到的两名观众都喜爱该演讲的概率.
附:临界值表
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.705 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
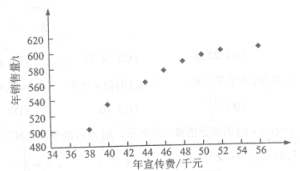
【题目】(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() =
=![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,![]() 与
与![]()
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(III)已知这种产品的年利润z与x,y的关系为![]() ,根据(Ⅱ)的结果回答下列问题:
,根据(Ⅱ)的结果回答下列问题:
(Ⅰ)当年宣传费![]() 时,年销售量及年利润的预报值时多少?
时,年销售量及年利润的预报值时多少?
(Ⅱ)当年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]()
(1) 证明:数列![]() 是等比数列;
是等比数列;
(2) 求使不等式![]() 成立的所有正整数m、n的值;
成立的所有正整数m、n的值;
(3) 如果常数0 < t < 3,对于任意的正整数k,都有![]() 成立,求t的取值范围.
成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
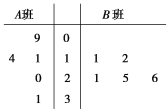
【题目】某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
(1) 试估计哪个班级学生平均上网的时间较长。
(2)从A班的样本数据中随机抽取一个不超过19的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com