
分析 由题意可得b-1>0且a+(b-1)=1,整体代入可得$\frac{4}{a}$+$\frac{1}{b-1}$=($\frac{4}{a}$+$\frac{1}{b-1}$)[a+(b-1)]=5+$\frac{4(b-1)}{a}$+$\frac{a}{b-1}$,由基本不等式可得.
解答 解:∵a>0,b>1,且a+b=2,
∴b-1>0且a+(b-1)=1,
∴$\frac{4}{a}$+$\frac{1}{b-1}$=($\frac{4}{a}$+$\frac{1}{b-1}$)[a+(b-1)]
=5+$\frac{4(b-1)}{a}$+$\frac{a}{b-1}$≥5+2$\sqrt{\frac{4(b-1)}{a}•\frac{a}{b-1}}$=9,
当且仅当$\frac{4(b-1)}{a}$=$\frac{a}{b-1}$时取等号,
结合a+(b-1)=1可解得a=$\frac{2}{3}$且b=$\frac{4}{3}$,
故所求最小值为9
故答案为:9
点评 本题考查基本不等式求最值,整体代入是解决问题的关键,属基础题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 0 | C. | -2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a+b)2≤4ab,$a+b≤\sqrt{2{a^2}+2{b^2}}$ | B. | (a+b)2≥4ab,$a+b≤\sqrt{2{a^2}+2{b^2}}$ | ||
| C. | (a+b)2≤4ab,$a+b≥\sqrt{2{a^2}+2{b^2}}$ | D. | (a+b)2≥4ab,$a+b≥\sqrt{2{a^2}+2{b^2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 命题“?x≥0,x2+x-1<0”的否定是“?x<0,x2+x-1<0” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | 若命题p为真命题,则命题¬p也可能为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
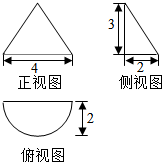
| A. | $(4+2\sqrt{13})π$ | B. | $6+(2+\sqrt{13})π$ | C. | $(\sqrt{13}+2)π$ | D. | $8+2\sqrt{13}π$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com