
思路解析:这个问题的通用解法称为“孙子剩余定理”或“中国剩余定理”。著名的“韩信点兵问题”即为此例的应用。
设物共m个,被3,5,7除所得的商分别为x、y、z,则这个问题相当于求不定方程
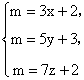 的正整数解。m应同时满足下列三个条件:(1)mMOD 3=2;(2)mMOD 5=3;(3)mMOD 7=2。因此,可以让m从2开始检验,若3个条件中有任何一个不成立,则m递增1,一直到m同时满足三个条件为止。考虑到m被7除余数为2,故m至少是9,也可以从m=9开始验证。
的正整数解。m应同时满足下列三个条件:(1)mMOD 3=2;(2)mMOD 5=3;(3)mMOD 7=2。因此,可以让m从2开始检验,若3个条件中有任何一个不成立,则m递增1,一直到m同时满足三个条件为止。考虑到m被7除余数为2,故m至少是9,也可以从m=9开始验证。
答案:m=2
f=0
WHILE f=0
IF mMOD 3=2 AND mMOD 5=3
AND mMOD 7=2 THEN
PRINT “物体的个数为:”;m
f=1
ELSE
m=m+1
END IF
WEND
END


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修3 1.4算法案例练习卷(解析版) 题型:解答题
我国《算经十书》之一《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?答曰:二十三.”你能用程序解决这个问题吗?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年贵州省黔西南州贞丰三中高二(上)8月月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年贵州省黔西南州册亨二中高二(上)8月月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com