
����Ŀ��ij���Ĺ�˾��![]() ��
��![]() ���ظ���һ�ҹ��������������Ľ����ɹ�˾ֱ������
���ظ���һ�ҹ��������������Ľ����ɹ�˾ֱ������![]() ��.������·��ͨ���䲻�㣬Ϊ�˼����˷ѣ��ù�˾Ԥ��Ͷ����һ����
��.������·��ͨ���䲻�㣬Ϊ�˼����˷ѣ��ù�˾Ԥ��Ͷ����һ����![]() �ػ�
�ػ�![]() ��ֱ��
��ֱ��![]() �صĹ�·����ѡ���ij������·��������һ�������Ľ��Ŀ����������õ�������
�صĹ�·����ѡ���ij������·��������һ�������Ľ��Ŀ����������õ�������![]() �Խ�Լ����.��֪
�Խ�Լ����.��֪![]() ��
��![]() ֮��Ϊ��·����·�˷�Ϊÿ��ǧ��20Ԫ����·���˷Ѽ��룬
֮��Ϊ��·����·�˷�Ϊÿ��ǧ��20Ԫ����·���˷Ѽ��룬![]() ��
��![]() ��
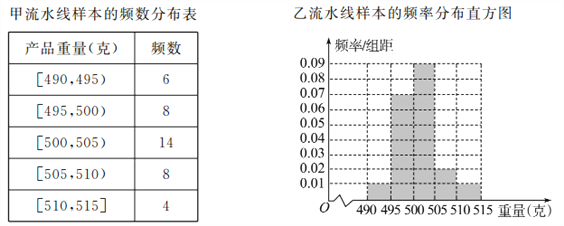
��![]() ���ؾ�����ͼ��ʾ.Ϊ���ƶ���·�ƻ�����˾ͳ�������10����������ÿ��Ľ��IJ������õ����������ͼ�����������������10���ղ�����Ƶ�ʴ����ղ����ĸ���.
���ؾ�����ͼ��ʾ.Ϊ���ƶ���·�ƻ�����˾ͳ�������10����������ÿ��Ľ��IJ������õ����������ͼ�����������������10���ղ�����Ƶ�ʴ����ղ����ĸ���.
��1����![]() ��
��![]() ���ع���ij������ղ���Ϊ20�֡��ĸ��ʣ�
���ع���ij������ղ���Ϊ20�֡��ĸ��ʣ�
��2������·��ÿ���ܵ��˷ѵ�����Ϊ���ݣ��жϴ�![]() ��
��![]() ��һ����·���ӻ���.
��һ����·���ӻ���.

���𰸡�(1) ![]() ;(2) ��
;(2) ��![]() ����·������.
����·������.
�������������������1������֪�ɵ��������![]() .
.
��2��ͬ���ɵ�![]() ��
��![]() ���ع���ij������ղ���Ϊ19�֣�21�ֵĸ��ʷֱ�Ϊ
���ع���ij������ղ���Ϊ19�֣�21�ֵĸ��ʷֱ�Ϊ![]() ��
��![]() ���Ӷ����
���Ӷ����
��![]() ����·����
����·����![]() �ص�
�ص�![]() ��ÿ����˷ѵ�����Ϊ
��ÿ����˷ѵ�����Ϊ![]() ��Ԫ������
��Ԫ������![]() �ص�
�ص�![]() ��ÿ����˷ѵ�����Ϊ��
��ÿ����˷ѵ�����Ϊ��
![]() ��Ԫ������˴�
��Ԫ������˴�![]() ����·��ÿ������˷ѵ�����Ϊ��
����·��ÿ������˷ѵ�����Ϊ��![]() ��Ԫ����ͬ���ɵô�
��Ԫ����ͬ���ɵô�![]() ����·��ÿ������˷ѵ�����Ϊ��
����·��ÿ������˷ѵ�����Ϊ��![]() ��Ԫ��.���ϣ���
��Ԫ��.���ϣ���![]() ����·������.
����·������.
�����������1���衰![]() ��
��![]() ���ع�˾���ղ���Ϊ20�֡�Ϊ�¼�
���ع�˾���ղ���Ϊ20�֡�Ϊ�¼�![]() ��
��
��![]() .
.
��2��ͬ������![]() ��
��![]() ���ع���ij������ղ���Ϊ19�֣�21�ֵĸ��ʷֱ�Ϊ
���ع���ij������ղ���Ϊ19�֣�21�ֵĸ��ʷֱ�Ϊ![]() ��
��![]() .
.
����![]() ����·����
����·����![]() �ص�
�ص�![]() ��ÿ����˷ѵ�����Ϊ��
��ÿ����˷ѵ�����Ϊ��![]() ��Ԫ��.
��Ԫ��.
��![]() �ص�
�ص�![]() ��ÿ����˷ѵ�����Ϊ��
��ÿ����˷ѵ�����Ϊ��
![]()
![]() ��Ԫ��.
��Ԫ��.
���Դ�![]() ����·��ÿ������˷ѵ�����Ϊ��
����·��ÿ������˷ѵ�����Ϊ��![]() ��Ԫ��.
��Ԫ��.
����![]() ����·����
����·����![]() �ص�
�ص�![]() ��ÿ����˷ѵ�����Ϊ��
��ÿ����˷ѵ�����Ϊ��![]() .
.
��![]() �ص�
�ص�![]() ��ÿ����˷ѵ�����Ϊ��
��ÿ����˷ѵ�����Ϊ��
![]()
![]() ��Ԫ��.
��Ԫ��.
���Դ�![]() ����·��ÿ������˷ѵ�����Ϊ��
����·��ÿ������˷ѵ�����Ϊ��![]() ��Ԫ��.
��Ԫ��.
���Դ�![]() ����·������.
����·������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʳƷ��Ϊ�˼��ס��������Զ���װ��ˮ�ߵ�����������������������ˮ���ϸ���ȡ40����Ʒ��Ϊ���������Ƴ����ǵ���������λ���ˣ�������ֵ����![]() �ڵIJ�ƷΪ�ϸ�Ʒ������Ϊ���ϸ�Ʒ��ͳ�ƽ�������
�ڵIJ�ƷΪ�ϸ�Ʒ������Ϊ���ϸ�Ʒ��ͳ�ƽ�������
���������ˮ�������ϸ��Ƶ�ʣ�
��������ˮ��������ֵ����![]() �ڵIJ�Ʒ����ȡ2����Ʒ������2����Ʒ��ǡ��ֻ��һ���ϸ�ĸ��ʣ�
�ڵIJ�Ʒ����ȡ2����Ʒ������2����Ʒ��ǡ��ֻ��һ���ϸ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�����߳��ɵȲ����У�����Ϊ2�������ǵ�����ֵΪ ![]() ������������ε��ܳ��ǣ� ��
������������ε��ܳ��ǣ� ��
A.9
B.12
C.15
D.18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
��1����![]() ����
����![]() ����Сֵ��
����Сֵ��
��2��������![]() ��
��![]() ����һ������
����һ������![]() ��֤��������
��֤��������![]() ��
��![]() �ڵ�
�ڵ�![]() ������ͬ�����ߣ���
������ͬ�����ߣ���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˫���� ![]() =1��a��0��b��0����������Ϊ2������ԭ�㵽ֱ��AB�ľ���Ϊ
=1��a��0��b��0����������Ϊ2������ԭ�㵽ֱ��AB�ľ���Ϊ ![]() ������A��a��0����B��0����b����
������A��a��0����B��0����b����
��1����˫���ߵķ��̣�
��2����B1��˫����������y���������ϵĶ˵㣬��B��ֱ����˫���߽���M��N���㣬��B1M��B1Nʱ��ֱ��MN�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����p������x2+y2��ax+y+1=0��ʾԲ������q������2ax+��1��a��y+1=0��ʾб�ʴ���1��ֱ�ߣ���p��qΪ�����⣬p��qΪ�����⣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����C�� ![]() =1��������Ϊ
=1��������Ϊ ![]() ���㣨
���㣨 ![]() ��0����˫���ߵ�һ�����㣮
��0����˫���ߵ�һ�����㣮
��1����˫���ߵķ��̣�
��2��������˫�����ҽ���F2����б��Ϊ30��ֱ��l��ֱ��l��˫���߽��ڲ�ͬ��A��B���㣬��AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��1�� ![]() ������ԲE��
������ԲE�� ![]() =1�ϣ���б��Ϊ
=1�ϣ���б��Ϊ ![]() ��ֱ��l����ԲE����B��C���㣬����ABC��������ʱ����ֱ��l�ķ��̣�
��ֱ��l����ԲE����B��C���㣬����ABC��������ʱ����ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ʳ������ס������ֻ�Ϸ��ϣ�����1��Ƥ���ַ��ϵ���Ҫԭ����������4t��������18t������1�����ַ��ϵ���Ҫԭ����������1t��������15t���ֿ��������10t��������66t����֪����1��Ƥ���ַ��ϣ�����������Ϊ10000Ԫ������1��Ƥ���ַ��ϣ�����������Ϊ5000Ԫ����ô�ֱ������ס������ַ��ϸ����ٳ�Ƥ���ܹ��������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com