
【题目】已知函数![]()
(Ⅰ)若函数![]() 的图像在点
的图像在点![]() 处的切线与直线
处的切线与直线![]() 平行,求实数
平行,求实数![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调性;
的单调性;
(Ⅲ)若在函数![]() 定义域内,总有
定义域内,总有![]() 成立,试求实数
成立,试求实数![]() 的最大值.
的最大值.
【答案】(Ⅰ) ![]() ;(Ⅱ)证明见解析;(Ⅲ)
;(Ⅱ)证明见解析;(Ⅲ) ![]()
【解析】试题分析:(1)先根据导数几何意义得![]() ,解得实数
,解得实数![]() 的值;(2)求导数并分解因式,根据a与1的大小分类讨论导函数符号,根据导函数符号确定函数
的值;(2)求导数并分解因式,根据a与1的大小分类讨论导函数符号,根据导函数符号确定函数![]() 的单调性;(3)先化简不等式,并根据不等式恒成立转化为对应函数最值问题:
的单调性;(3)先化简不等式,并根据不等式恒成立转化为对应函数最值问题: ![]() 最大值不大于零,再利用导数求得函数最值
最大值不大于零,再利用导数求得函数最值![]()
从而有![]() 的最大值,最后利用导数求得
的最大值,最后利用导数求得![]() 最大值,即得实数
最大值,即得实数![]() 的最大值.
的最大值.
试题解析:(Ⅰ)易得![]() ,且
,且![]()
由题意,得![]() ,解得
,解得![]() ,
,
(Ⅱ)由(Ⅰ)得![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() 函数
函数![]() 在
在![]() 单调递减,
单调递减,
②当![]() 时,由
时,由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() 或
或![]()
![]() 函数
函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
③当![]() 时,同理,得
时,同理,得
函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
综上,当![]() 时,函数
时,函数![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅲ)由题意,知![]() 恒成立,
恒成立,
![]() 恒成立,
恒成立,
![]() 恒成立,
恒成立,
令![]() ,则只需
,则只需![]()
![]() ,
,
由![]() ,得
,得![]() ,
,
![]() 当
当![]() 时,
时, ![]() ,此时,函数
,此时,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,此时,函数
,此时,函数![]() 在
在![]() 上单调递减,
上单调递减,
![]()
![]()
令![]() ,则只需
,则只需![]()
![]()
由![]() ,得
,得![]() ,此时,
,此时, ![]() 在
在![]() 上单调递减,
上单调递减,
由![]() ,得
,得![]() ,此时,
,此时, ![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,
即![]()
故所求实数![]() 的最大值为
的最大值为![]()


科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,若
,若![]() ,有
,有![]() ,则称函数
,则称函数![]() 为定义在
为定义在![]() 上的非严格单增函数;若
上的非严格单增函数;若![]() ,有
,有![]() ,则称函数
,则称函数![]() 为定义在
为定义在![]() 上的非严格单减函数.
上的非严格单减函数. ![]() .
.
(1)若函数![]() 为定义在
为定义在![]() 上的非严格单增函数,求实数
上的非严格单增函数,求实数![]() 的取值范围.
的取值范围.
(2)若函数![]() 为定义在
为定义在![]() 上的非严格单减函数,试解不等式
上的非严格单减函数,试解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |

(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】所谓正三棱锥,指的是底面为正三角形,顶点在底面上的射影为底面三角形中心的三棱锥,在正三棱锥S﹣ABC中,M是SC的中点,且AM⊥SB,底面边长AB=2 ![]() ,则正三棱锥S﹣ABC的体积为 , 其外接球的表面积为 .
,则正三棱锥S﹣ABC的体积为 , 其外接球的表面积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:x1 , x2是方程x2﹣mx﹣1=0的两个实根,且不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立;命题q:不等式ax2+2x﹣1>0有解,若命题p∨q为真,p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式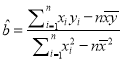 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿海准备购买“海马”牌一辆小汽车,其中购车费用12.8万元,每年的保险费、汽油费约为0.95万元,年维修、保养费第一年是0.1万元,以后逐年递增0.1万元.请你帮阿海计算一下这种汽车使用多少年,它的年平均费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com