
【题目】已知直三棱柱ABC﹣A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=3,∠BAC=120°,AA1=8,则球O的表面积为( )
A.25πB.![]() πC.100πD.
πC.100πD.![]() π
π
科目:高中数学 来源: 题型:
【题目】某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.

(1)若该蛋糕店某一天制作生日蛋糕17个,设当天的需求量为![]() ,则当天的利润
,则当天的利润![]() (单位:元)是多少?
(单位:元)是多少?
(2)若蛋糕店一天制作17个生日蛋糕.
①求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() 的函数解析式;
的函数解析式;
②求当天的利润不低于600圆的概率.
(3)若蛋糕店计划一天制作16个或17个生日蛋糕,请你以蛋糕店一天利润的平均值作为决策依据,应该制作16个还是17个生日蛋糕?
查看答案和解析>>
科目:高中数学 来源: 题型:
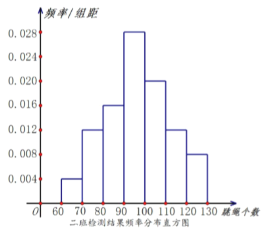
【题目】某小学六年级学生的进行一分钟跳绳检测,现一班二班各有50人,根据检测结果绘出了一班的频数分布表和二班的频率分布直方图.
一班检测结果频数分布表:
跳绳个数区间 |
|
|
|
|
|
频数 | 7 | 13 | 20 | 8 | 2 |
(1)根据给出的图表估计一班和二班检测结果的中位数(结果保留两位小数);
(2)跳绳个数不小于100个为优秀,填写下面2×2列联表,并根据列联表判断是否有95%的把握认为检测结果是否优秀与班级有关.
一班 | 二班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式及数据: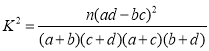 ,
,
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的离心率为
1(a>b>0)的离心率为![]() ,O是坐标原点,点A,B分别为椭圆C的左右顶点,|AB|=4
,O是坐标原点,点A,B分别为椭圆C的左右顶点,|AB|=4![]() .
.
(1)求椭圆C的标准方程.
(2)若P是椭圆C上异于A,B的一点,直线l交椭圆C于M,N两点,AP∥OM,BP∥ON,则△OMN的面积是否为定值?若是,求出定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北、湖北,从西部选择宁夏,从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区,在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记,由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验,在某普查小区,共有50家企事业单位,150家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 100 | 50 | 150 |
合计 | 140 | 60 | 200 |
(1)写出选择5个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)以该小区的个体经营户为样本,频率作为概率,从全国个体经营户中随机选择3家作为普查对象,入户登记顺利的对象数记为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() 的期望值.
的期望值.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有A,B、C、D四人先后感染了新型冠状病毒,其中只有A到过疫区,B肯定是受A感染的,对于C,因为难以判定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是![]() ,同样也假设D受A、B和C感染的概率都是
,同样也假设D受A、B和C感染的概率都是![]() .在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的可能取值为______,并求X的均值(即数学期望)为______.
.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的可能取值为______,并求X的均值(即数学期望)为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中把三角形的田称为“圭田”,把直角梯形的田称为“邪田”,称底是“广”,称高是“正从”,“步”是丈量土地的单位.现有一邪田,广分别为十步和二十步,正从为十步,其内有一块广为八步,正从为五步的圭田.若在邪田内随机种植一株茶树,求该株茶树恰好种在圭田内的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com