
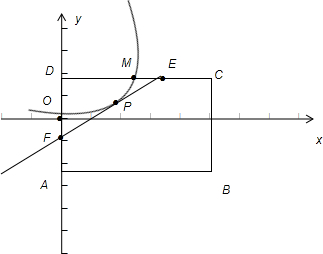
 如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,向如何画切割线EF可使剩余部分五边形ABCEF的面积最大?
如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,向如何画切割线EF可使剩余部分五边形ABCEF的面积最大?
| ||
| 6 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1+4t2 |
| 8t |
| 1 |
| 4 |
| 1 |
| 2 |
| 1+4t2 |
| 8t |
| 1 |
| 4 |
| 16t4+8t2+1 |
| 64t |
| 1 |
| 2 |
| S | ′ △EFD |
| 1 |
| 64 |
| 48t2+8t2-1 |
| t2 |
| (12t2-1)(4t2+1) |
| 64t2 |
3(4t2+1)(t+
| ||||||||
| 16t2 |
| ||
| 6 |
| ||
| 6 |
| 1 |
| 2 |
| ||
| 6 |
| ||
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
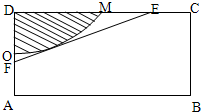 如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米.
如图,有一矩形钢板ABCD缺损了一角(图中阴影部分),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1米,AD=0.5米,当沿切割线EF切割使剩余部分五边形ABCEF的面积最大时,AF的长度为( )米.A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源:黑龙江省牡丹江一中09-10学年高二下学期期中考试实验班(数学理) 题型:选择题
如图,有一矩形钢板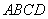 缺损了一角(图中阴影部分),边缘线
缺损了一角(图中阴影部分),边缘线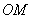 上每一点到点
上每一点到点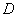 的距离都等于它到边
的距离都等于它到边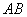 的距离。工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若
的距离。工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若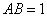 米,
米,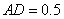 米,当沿切割线
米,当沿切割线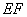 切割使剩余部分五边形
切割使剩余部分五边形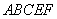 的面积最大时,
的面积最大时,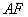 的长度为( )米。
的长度为( )米。
 A
A
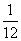 B
B
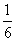
C
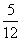 D
D
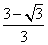
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com