
����Ŀ������Ϊһ���罻�����Ѿ���֧�������ƣ���ͨ���˶��ȸ�������˵�����������ָ����ı���.�ֻ����еġ����˶������������Կ��Լ�ÿ����˶������������Կ�������Ȧ����ѵIJ���. ![]() ��������Ȧ���д�������ʹ���ˡ����˶��������.�����ѡȡ������40������¼������ijһ�����·������ͳ���������±���ʾ��
��������Ȧ���д�������ʹ���ˡ����˶��������.�����ѡȡ������40������¼������ijһ�����·������ͳ���������±���ʾ��

��1���������������壬������Ƶ��Ϊ���ʣ���![]() ������������Ȧ������Ժ���������ѡȡ3����������·����������6000������
������������Ȧ������Ժ���������ѡȡ3����������·����������6000������![]() ������
������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
��2�����ij��һ�����·����������8000�������˽��������˶�������Ϊ���˶����ˡ�������Ϊ���˶����ˡ�.����������������![]() �����������ݴ��ж��ܷ���90%���ϵİ�����Ϊ���������͡�
�����������ݴ��ж��ܷ���90%���ϵİ�����Ϊ���������͡�
�롰�Ա��йأ�

����![]() .
.

���𰸡���1������������2��������
��������
��1����ȷ��X��ȡֵ������������ʣ��õ��ֲ��к�������
��2���������ݣ����㿨�����ó�����.
��1����С�������Ժ���������ȡ1��.������·����������6000�ĸ���Ϊ![]() ����ȡֵ�ֱ�Ϊ0��1��2��3.
����ȡֵ�ֱ�Ϊ0��1��2��3.
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��![]() .
.
�������![]()
![]() ��
��
��2�����![]() ������
������
�˶����� | �˶����� | �ܼ� | |
�� | 6 | 14 | 20 |
Ů | 4 | 16 | 20 |
�ܼ� | 10 | 30 | 40 |
![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]()
![]() .
.
�ݴ��ж�û��![]() ���ϵİ�����Ϊ���������͡��롰�Ա��й�.��
���ϵİ�����Ϊ���������͡��롰�Ա��й�.��


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
��1����a=0ʱ������f��x���ڣ�1��f��1�����������߷��̣�
��2����![]() ����
����![]() �ļ�ֵ.
�ļ�ֵ.
��3����![]() ����ʵ��
����ʵ��![]() ����
����![]() ��
��
֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ���ⳤΪ2�������壬
���ⳤΪ2�������壬![]() Ϊ��Խ���
Ϊ��Խ���![]() �ϵĶ��㣨�������˵㣩��
�ϵĶ��㣨�������˵㣩��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() .
.

��1�����÷�֤��֤��ֱ��![]() ��
��![]() ������ֱ�ߣ�
������ֱ�ߣ�
��2����![]() ����
����![]() ����ʾΪ
����ʾΪ![]() �ĺ���
�ĺ���![]() ������˺�����ֵ��
������˺�����ֵ��
��3����![]() ��Сʱ��������ֱ��
��Сʱ��������ֱ��![]() ��
��![]() ���ɽǵĴ�С.
���ɽǵĴ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����λͬѧ��ҵ��������һЩС�ҵ������������ÿ����������۵�����ܻ𱬣������������˾���������ѧרҵ����������ҵ��ר����������С�ҵ���������뾭����ǩ���˾�����ͬ��������������С�ҵ��������ÿ��![]() Ԫ�ļ۸�ȫ���ɾ����̰���.���г����У��������������ÿ����ҪͶ��̶��ɱ�Ϊ
Ԫ�ļ۸�ȫ���ɾ����̰���.���г����У��������������ÿ����ҪͶ��̶��ɱ�Ϊ![]() ��Ԫ��ÿ����
��Ԫ��ÿ����![]() ��������������Ͷ���ʽ�
��������������Ͷ���ʽ�![]() ��Ԫ.���²�������
��Ԫ.���²�������![]() ���ʱ��
���ʱ��![]() ����Ԫ�������²�����С��
����Ԫ�������²�����С��![]() ���ʱ��
���ʱ��![]() ����Ԫ��.��֪�²�����
����Ԫ��.��֪�²�����![]() ���ʱ����Ҫ��Ͷ����ʽ���
���ʱ����Ҫ��Ͷ����ʽ���![]() ��Ԫ.
��Ԫ.
��1���Խ�������ЩС�ҵ��������![]() ����Ԫ����ʾ���²���
����Ԫ����ʾ���²���![]() ��������ĺ�������ע��������
��������ĺ�������ע��������![]() ����������
����������![]() �̶��ɱ�
�̶��ɱ�![]() ��Ͷ��ɱ���
��Ͷ��ɱ���
��2���²���Ϊ�������ʱ������λͬѧ������Щ�����õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C�Ľ�����y���ϣ����㵽�ߵľ���Ϊ2���ҶԳ���Ϊy��.
��1����������C�ı����̣�
��2����������C�Ľ���Ϊ![]() ʱ����F��ֱ�߽��������ڣ�A��B���㣬��ֱ��OA��OB��OΪ����ԭ�㣩�ֱ�ֱ��
ʱ����F��ֱ�߽��������ڣ�A��B���㣬��ֱ��OA��OB��OΪ����ԭ�㣩�ֱ�ֱ��![]() ��M��N���㣬��
��M��N���㣬��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
������![]() ����
����![]() �ľ��������ֱ��
�ľ��������ֱ��![]() �ľ�����ȣ��ǵ�
�ľ�����ȣ��ǵ�![]() �Ĺ켣Ϊ
�Ĺ켣Ϊ![]() .
.
��1����![]() �ķ��̣�
�ķ��̣�
��2�����![]() ������
������![]() �ϣ�
�ϣ�![]() ����һ��
����һ��![]() ���ڵ�
���ڵ�![]() �Ҳࣩ����
�Ҳࣩ����![]() ����ƽ����
����ƽ����![]() ��ֱ��������
��ֱ��������![]() �����ڵ�
�����ڵ�![]() �����ж�ֱ��
�����ж�ֱ��![]() �Ƿ����
�Ƿ����![]() ����˵������.
����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
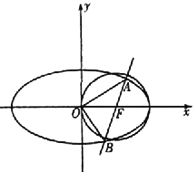
����Ŀ����ͼ����ԲG������������ԭ�㣬����һ������ΪԲF��x2+y2��2x��0��Բ�ģ��Ҷ�����ԲF��x���һ�����㣮��֪��ԲG��ֱ��l��x��my��1��0�ཻ��A��B���㣮
��I������Բ�ķ��̣�
�������AOB��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ƽ���ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����ʹ
����ʹ![]() ������
������![]() ��
��![]() ���õ���ͼ����ʾ�ļ����壮
���õ���ͼ����ʾ�ļ����壮

��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2������![]() ���߶�
���߶�![]() �ϣ�ֱ��
�ϣ�ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ��������
��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����
����![]() ����Բ
����Բ![]() �ϣ���
�ϣ���![]() ����Сֵ��
����Сֵ��![]() ��
��![]() Ϊ����ԭ�㣩.
Ϊ����ԭ�㣩.
��1������Բ![]() �ı�����.
�ı�����.
��2����֪��ֱ��![]() ��Բ
��Բ![]() ��
��![]() ���У�������Բ
���У�������Բ![]() ����
����![]() ��
��![]() ����.�Ƿ����ʵ��
����.�Ƿ����ʵ��![]() ��ʹ��
��ʹ��![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com