
【题目】已知如图,矩形![]() 所在平面与底面
所在平面与底面![]() 垂直,在直角梯形
垂直,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
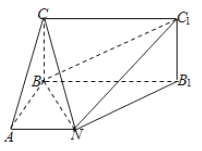
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)根据题意可得![]() ,再根据线面平行的判定定理即可证明;
,再根据线面平行的判定定理即可证明;
(2)根据题意证出![]() ,
,![]() ,然后根据线面垂直的判定定理证明即可;
,然后根据线面垂直的判定定理证明即可;
(3)过![]() 作
作![]() 交
交![]() 于
于![]() ,结合题意证明
,结合题意证明![]() 为
为![]() 与平面
与平面![]() 所成角的平面角后,即可求出
所成角的平面角后,即可求出![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
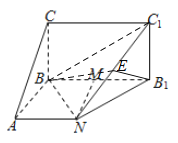
(1)![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)取![]() 中点为
中点为![]() ,连接
,连接![]() ,
,
又![]()
![]() ,
,![]() ,
,![]() 且
且![]() ,
,
![]() 边形
边形![]() 为正方形,
为正方形,![]() 为直角三角形,
为直角三角形,
可得![]() ,
,
又![]() ,
,
![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,且四边形
,且四边形![]() 为矩形,
为矩形,
![]()
平面![]() 平面
平面![]()
![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,
,
![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() .
.
(3)过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
由(2)知![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
![]() ,
,
![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
因此![]() 为
为![]() 与平面
与平面![]() 所成角的平面角,
所成角的平面角,
在![]() 中,
中,![]() ,
,![]() ,
,
可得![]() ,
,
又![]() ,
,
![]() ,
,
在![]() 中,
中,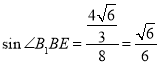 .
.
所以![]() 与平面
与平面![]() 所成角的正弦值为:
所成角的正弦值为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,《数书九章》中记录了秦九昭的许多创造性成就,其中在卷五“三斜求积”中提出了已知三角形三边![]() ,
,![]() ,
,![]() 求面积的公式,这与古希腊的海伦公式完成等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”若把以上这段文字写成公式,即
求面积的公式,这与古希腊的海伦公式完成等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”若把以上这段文字写成公式,即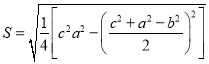 .现有
.现有![]() 满足
满足![]() ,且
,且![]() 的面积
的面积![]() ,请运用上述公式判断下列命题正确的是
,请运用上述公式判断下列命题正确的是
A.![]() 周长为
周长为![]()
B.![]() 三个内角
三个内角![]() ,
,![]() ,
,![]() 成等差数列
成等差数列
C.![]() 外接圆直径为
外接圆直径为![]()
D.![]() 中线
中线![]() 的长为
的长为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是给定的平面,设不在
是给定的平面,设不在![]() 内的任意两点M,N所在的直线为l,则下列命题正确的是( )
内的任意两点M,N所在的直线为l,则下列命题正确的是( )
A.在![]() 内存在直线与直线l异面
内存在直线与直线l异面
B.在![]() 内存在直线与直线l相交
内存在直线与直线l相交
C.在![]() 内存在直线与直线l平行
内存在直线与直线l平行
D.存在过直线l的平面与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量![]() 满足
满足![]() ,则以下说法正确的有( )个.
,则以下说法正确的有( )个.
①![]() ;
;
②对于平面内任一向量![]() ,有且只有一对实数
,有且只有一对实数![]() ,
,![]() 使
使![]() ;
;
③若![]() ,且
,且![]() ,则
,则![]() 的范围为
的范围为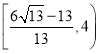 ;
;
④设![]() ,且
,且![]() 在
在![]() 处取得最小值,当
处取得最小值,当![]() 时,则
时,则![]() ;
;
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中不可或缺的一部分![]() 市某调查机构针对该市市场占有率最高的两种网络外卖企业
市某调查机构针对该市市场占有率最高的两种网络外卖企业![]() 以下简称外卖A、外卖
以下简称外卖A、外卖![]() 的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
分数 人数 种类 |
|
|
|
|
|
外卖A | 50 | 150 | 100 | 400 | 300 |
外卖B | 100 | 100 | 300 | 200 | 300 |
表中得分越高,说明市民对网络外卖服务越满意![]() 若得分不低于60分,则表明该市民对网络外卖服务质量评价较高
若得分不低于60分,则表明该市民对网络外卖服务质量评价较高![]() 现将分数按“服务质量指标”划分成以下四个档次:
现将分数按“服务质量指标”划分成以下四个档次:
分数 |
|
|
|
|
服务质量指标 | 0 | 1 | 2 | 3 |
视频率为概率,解决下列问题:
![]() 从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
![]() 从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
![]() 在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的右焦点坐标为
的右焦点坐标为![]() ,且点
,且点![]() 在C上.
在C上.
(1)求椭圆的方程;
(2)过点![]() 的直线l与C交于M,N两点,P为线段MN的中点,A为C的左顶点,求直线AP的斜率k的取值范围.
的直线l与C交于M,N两点,P为线段MN的中点,A为C的左顶点,求直线AP的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中![]() 点表示十月的平均最高气温约为
点表示十月的平均最高气温约为![]() ,
,![]() 点表示四月的平均最低气温约为
点表示四月的平均最低气温约为![]() .下面叙述不正确的是( )
.下面叙述不正确的是( )

A.各月的平均最高气温都在![]() 以上
以上
B.六月的平均温差比九月的平均温差大
C.七月和八月的平均最低气温基本相同
D.平均最低气温高于![]() 的月份有5个
的月份有5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com