
【题目】为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后,发布了《个人所得税专项附加扣除暂行办法》,明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用,并公布了相应的定额扣除标准,决定自2019年1月1日起施行,某机关为了调查内部职员对新个税方案的满意程度与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁及以下 | 40岁以上 | 合计 | |
基本满意 | 15 | 30 | 45 |
很满意 | 25 | 10 | 35 |
合计 | 40 | 40 | 80 |
(1)根据列联表,能否有99%的把握认为满意程度与年龄有关?
(2)为了帮助年龄在40岁以下的未购房的8名员工解决实际困难,该企业拟员工贡献积分![]() (单位:分)给予相应的住房补贴
(单位:分)给予相应的住房补贴![]() (单位:元),现有两种补贴方案,方案甲:
(单位:元),现有两种补贴方案,方案甲:![]() ;方案乙:
;方案乙: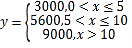 .已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“
.已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“![]() 类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“
类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“![]() 类员工”的概率。
类员工”的概率。
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)见解析(2)![]()
【解析】
(1)由列联表计算![]() 的观测值即可求解;(2)由题得8名员工的贡献积分及按甲、乙两种方案所获补贴情况,进一步得到“
的观测值即可求解;(2)由题得8名员工的贡献积分及按甲、乙两种方案所获补贴情况,进一步得到“![]() 类员工”的人数,再利用古典概型求解即可
类员工”的人数,再利用古典概型求解即可
(1)根据列联表可以求得![]() 的观测值:
的观测值:
![]() .
.
∵![]() .
.
∴有99%的把握认为满意程度与年龄有关
(2)据题意,该8名员工的贡献积分及按甲、乙两种方案所获补贴情况为:
积分 | 2 | 3 | 6 | 7 | 7 | 11 | 12 | 12 |
方案甲 | 2400 | 3100 | 5200 | 5900 | 5900 | 8700 | 9400 | 9400 |
方案乙 | 3000 | 3000 | 5600 | 5600 | 5600 | 9000 | 9000 | 9000 |
由表可知,“![]() 类员工”有5名.
类员工”有5名.
设从这8名员工中随机抽取4名进行面谈,恰好抽到3名“![]() 类员工”的概率为
类员工”的概率为![]() .
.
则![]()
![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,椭圆![]() ,
,![]() 、
、![]() ,为椭圆
,为椭圆![]() 的左、右顶点.
的左、右顶点.

![]() 设
设![]() 为椭圆
为椭圆![]() 的左焦点,证明:当且仅当椭圆
的左焦点,证明:当且仅当椭圆![]() 上的点
上的点![]() 在椭圆的左、右顶点时,
在椭圆的左、右顶点时,![]() 取得最小值与最大值.
取得最小值与最大值.
![]() 若椭圆
若椭圆![]() 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为![]() ,最小值为
,最小值为![]() ,求椭圆
,求椭圆![]() 的标准方程.
的标准方程.
![]() 若直线
若直线![]() 与
与![]() 中所述椭圆
中所述椭圆![]() 相交于
相交于![]() 、
、![]() 两点(
两点(![]() 、
、![]() 不是左、右顶点),且满足
不是左、右顶点),且满足![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设X~N(μ1,![]() ),Y~N(μ2,
),Y~N(μ2,![]() ),这两个正态分布密度曲线如图所示,下列结论中正确的是 ( )
),这两个正态分布密度曲线如图所示,下列结论中正确的是 ( )
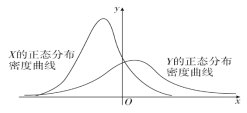
A. P(Y≥μ2)≥P(Y≥μ1)
B. P(X≤σ2)≤P(X≤σ1)
C. 对任意正数t,P(X≥t)≥P(Y≥t)
D. 对任意正数t,P(X≤t)≥P(Y≤t)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和点
和点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() ,
,![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于另一点
交于另一点![]() .给出以下判断:
.给出以下判断:
①直线![]() 与直线
与直线![]() 的斜率乘积为
的斜率乘积为![]() ;
;
②![]() 轴;
轴;
③以![]() 为直径的圆与抛物线准线相切.
为直径的圆与抛物线准线相切.
其中,所有正确判断的序号是( )
A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“五四青年节”到来之际,启东中学将开展一系列的读书教育活动.为了解高二学生读书教育情况,决定采用分层抽样的方法从高二年级![]() 四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
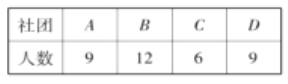
(1)若从参加问卷调查的12名学生中随机抽取2名,求这2名学生来自同一个社团的概率;
(2)在参加问卷调查的12名学生中,从来自![]() 三个社团的学生中随机抽取3名,用
三个社团的学生中随机抽取3名,用![]() 表示从
表示从![]() 社团抽得学生的人数,求
社团抽得学生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象上所有点的横坐标缩短到原来的
的图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),再将所得的图象向左平移
倍(纵坐标不变),再将所得的图象向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)写出函数![]() 的解析式;
的解析式;
(2)若对任意![]()
![]()
![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求实数![]() 和正整数
和正整数![]() ,使得
,使得![]() 在
在![]() 上恰有
上恰有![]() 个零点.
个零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com