
【题目】(![]() 分)已知椭圆
分)已知椭圆![]() 的左焦点为
的左焦点为![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.
两点.
(![]() )求椭圆
)求椭圆![]() 的离心率.
的离心率.
(![]() )当直线
)当直线![]() 与
与![]() 轴垂直时,求线段
轴垂直时,求线段![]() 的长.
的长.
(![]() )设线段
)设线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,直线
为坐标原点,直线![]() 交椭圆
交椭圆![]() 交于
交于![]() 、
、![]() 两点,是否存在直线
两点,是否存在直线![]() 使得
使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1) ![]() (2)
(2) ![]() (3) 存在直线
(3) 存在直线![]() ,使得
,使得![]() .
.
【解析】
试题分析:(1)将椭圆方程化为标准方程,求得a,b,c,进而得到离心率;(2)当直线l与x轴垂直时,即为x=﹣1,代入椭圆方程,求得纵坐标,进而得到弦长;(3)设直线AB:x=my﹣1,代入椭圆方程,可得(3+2m2)y2﹣4my﹣4=0,运用韦达定理,以及中点坐标公式可得P的坐标,再由向量共线的坐标表示,解方程可得m,进而判断存在这样是直线l.
解析:
(![]() )椭圆
)椭圆![]() ,
,
即为![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,
故椭圆的离心率![]() .
.
(![]() )当直线
)当直线![]() 与
与![]() 轴垂直时,即为
轴垂直时,即为![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() ,
,![]() ,
,
故线段![]() 的长为
的长为![]() .
.
(![]() )由
)由![]() ,设直线
,设直线![]() ,代入椭圆方程得
,代入椭圆方程得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
即有中点![]() 的坐标为
的坐标为![]() ,
,
直线![]() ,代入椭圆方程可得:
,代入椭圆方程可得:![]() ,
,
可设![]() ,
,![]() ,
,
假设存在直线![]() 使得
使得![]() ,
,
即有![]() ,
,
则![]() ,解得
,解得![]() ,
,
故存在直线![]() ,使得
,使得![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+a)lnx,g(x)= ![]() ,已知曲线y=f(x)在x=1处的切线过点(2,3).
,已知曲线y=f(x)在x=1处的切线过点(2,3).
(1)求实数a的值.
(2)是否存在自然数k,使得函数y=f(x)﹣g(x)在(k,k+1)内存在唯一的零点?如果存在,求出k;如果不存在,请说明理由.
(3)设函数h(x)=min{f(x),g(x)},(其中min{p,q}表示p,q中的较小值),对于实数m,x0∈(0,+∞),使得h(x0)≥m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
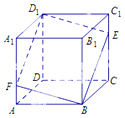
【题目】如图,在正方体![]() 中,点
中,点![]() 是棱
是棱![]() 上的一个动点,平面
上的一个动点,平面![]() 交棱
交棱![]() 于点
于点![]() .下列命题正确的为_______________.
.下列命题正确的为_______________.
①存在点![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②对于任意的点![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④对于任意的点![]() ,四棱锥
,四棱锥![]() 的体积均不变.
的体积均不变.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项为正的等比数列{an}的前n项和为Sn , S4=30,过点P(n,log2an)和Q(n+2,log2an+1)(n∈N*)的直线的一个方向向量为(﹣1,﹣1)
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn
,数列{bn}的前n项和为Tn , 证明:对于任意n∈N* , 都有Tn ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,
(1)求证:BD=DE;
(2)若∠ECA=45°,求AP2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥B﹣ACDE中,AE⊥平面ABC,CD∥AE,∠ABC=3∠BAC=90°,BF⊥AC于F,AC=4CD=4,AE=3.
(1)求证:BE⊥DF;
(2)求二面角B﹣DE﹣F的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们社会责任感与公众意识的不断提高,越来越多的人成为了志愿者.某创业园区对其员工是否为志愿者的情况进行了抽样调查,在随机抽取的10位员工中,有3人是志愿者.
(1)在这10人中随机抽取4人填写调查问卷,求这4人中恰好有1人是志愿者的概率P1;
(2)已知该创业园区有1万多名员工,从中随机调查1人是志愿者的概率为 ![]() ,那么在该创业园区随机调查4人,求其中恰有1人是志愿者的概率P2;
,那么在该创业园区随机调查4人,求其中恰有1人是志愿者的概率P2;
(3)该创业园区的A团队有100位员工,其中有30人是志愿者.若在A团队随机调查4人,则其中恰好有1人是志愿者的概率为P3 . 试根据(Ⅰ)、(Ⅱ)中的P1和P2的值,写出P1 , P2 , P3的大小关系(只写结果,不用说明理由).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对应的边分别为a,b,c.
(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,求cosB的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com