【答案】
分析:(I)根据f(x)为“一阶比增函数”不是“二阶比增函数”.可得g(x)=

=x
2-2hx-h,在(0,+∞)是增函数,且h(x)=

=x-2h-
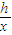
在(0,+∞)不是增函数,根据二次函数的图象和性质及导数法,可求出实数h的取值范围;
(Ⅱ)根据f(x)为“一阶比增函数”,且0<a<b<c,结合表中数据可得f(a)=d<

,f(b)=d<
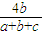
,f(c)=t<
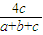
,根据不等式的性质可证得d(2d+t-4)>0;
(Ⅲ)根据f(x)为“二阶比增函数”,我们先证明f(x)≤0对x∈(0,+∞)成立,再证明f(x)=0在(0,+∞)上无解,综合两个证明结果,可得答案.
解答:解:(I)因为f(x)∈Ω
1,且f(x)∉Ω
2,
即g(x)=

=x
2-2hx-h,在(0,+∞)是增函数,所以h≤0 …(2分)
而h(x)=

=x-2h-
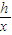
在(0,+∞)不是增函数,
又∵h′(x)=1+

,且
当h(x)是增函数时,有h≥0,所以当h(x)不是增函数时,h<0
综上,得h<0 …(4分)
证明:(Ⅱ) 因为f(x)∈Ω
1,且0<a<b<c<a+b+c,
所以
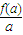
<

=
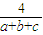
,所以f(a)=d<
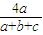
,
同理可证f(b)=d<
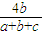
,f(c)=t<
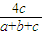
三式相加得f(a)+f(b)+f(c)=2d+t<
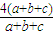
=4
所以2d+t-4<0 …(6分)
因为

<

,所以d(
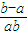
)<0
而0<a<b,所以d<0
所以d(2d+t-4)>0 …(8分)
(Ⅲ) 因为集合Φ={f(x)|f(x)∈Ω
2,且存在常数k,使得任取x∈(0,+∞),f(x)<k},
所以?f(x)∈Φ,存在常数k,使得 f(x)<k 对x∈(0,+∞)成立
我们先证明f(x)≤0对x∈(0,+∞)成立
假设?x
∈(0,+∞),使得f(x
)>0,
记

=m>0
因为f(x)是二阶比增函数,即

是增函数.
所以当x>x
时,
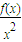
>
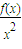
=m,所以f(x)>mx
2所以一定可以找到一个x
1>x
,使得f(x
1)>mx
12>k
这与f(x)<k 对x∈(0,+∞)成立矛盾 …(11分)
即f(x)≤0对x∈(0,+∞)成立
所以?f(x)∈Φ,f(x)≤0对x∈(0,+∞)成立
下面我们证明f(x)=0在(0,+∞)上无解
假设存在x
2>0,使得f(x
2)=0,
则因为f(x)是二阶增函数,即
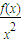
是增函数
一定存在x
3>x
2>0,使
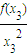
>
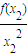
=0,这与上面证明的结果矛盾
所以f(x)=0在(0,+∞)上无解
综上,我们得到?f(x)∈Φ,f(x)<0对x∈(0,+∞)成立
所以存在常数M≥0,使得?f(x)∈Φ,?x∈(0,+∞),有f(x)<M成立
又令f(x)=-
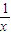
(x>0),则f(x)<0对x∈(0,+∞)成立,
又有

=

在(0,+∞)上是增函数,所以f(x)∈Φ,
而任取常数k<0,总可以找到一个x
n>0,使得x>x
n时,有有f(x)>k
所以M的最小值 为0 …(16分)
点评:本题考查的知识点是函数的单调性,导数的几何意义,全称命题,熟练掌握导数法在确定函数单调性和最值时的答题步骤是解答的关键.本题难度较大,运算量繁杂.

 在(0,+∞)上为增函数,则称f(x)为“一阶比增函数”;若y=
在(0,+∞)上为增函数,则称f(x)为“一阶比增函数”;若y= 在(0,+∞)上为增函数,则称f(x)为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为Ω1,所有“二阶比增函数”组成的集合记为Ω2.
在(0,+∞)上为增函数,则称f(x)为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为Ω1,所有“二阶比增函数”组成的集合记为Ω2. =x2-2hx-h,在(0,+∞)是增函数,且h(x)=
=x2-2hx-h,在(0,+∞)是增函数,且h(x)= =x-2h-
=x-2h-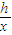 在(0,+∞)不是增函数,根据二次函数的图象和性质及导数法,可求出实数h的取值范围;
在(0,+∞)不是增函数,根据二次函数的图象和性质及导数法,可求出实数h的取值范围; ,f(b)=d<
,f(b)=d<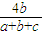 ,f(c)=t<
,f(c)=t<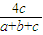 ,根据不等式的性质可证得d(2d+t-4)>0;
,根据不等式的性质可证得d(2d+t-4)>0; =x2-2hx-h,在(0,+∞)是增函数,所以h≤0 …(2分)
=x2-2hx-h,在(0,+∞)是增函数,所以h≤0 …(2分) =x-2h-
=x-2h-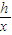 在(0,+∞)不是增函数,
在(0,+∞)不是增函数, ,且
,且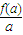 <
< =
=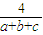 ,所以f(a)=d<
,所以f(a)=d<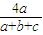 ,
,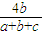 ,f(c)=t<
,f(c)=t<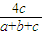
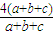 =4
=4 <
< ,所以d(
,所以d(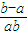 )<0
)<0  =m>0
=m>0 是增函数.
是增函数.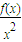 >
>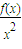 =m,所以f(x)>mx2
=m,所以f(x)>mx2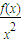 是增函数
是增函数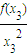 >
>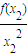 =0,这与上面证明的结果矛盾
=0,这与上面证明的结果矛盾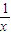 (x>0),则f(x)<0对x∈(0,+∞)成立,
(x>0),则f(x)<0对x∈(0,+∞)成立, =
= 在(0,+∞)上是增函数,所以f(x)∈Φ,
在(0,+∞)上是增函数,所以f(x)∈Φ,

