
【题目】已知f(x)=ex与g(x)=ax+b的图象交于P(x1 , y1),Q(x2 , y2)两点. (Ⅰ)求函数h(x)=f(x)﹣g(x)的最小值;
(Ⅱ)且PQ的中点为M(x0 , y0),求证:f(x0)<a<y0 .
【答案】解:(Ⅰ)h(x)=ex﹣ax﹣b,求导得h'(x)=ex﹣a 当a≤0时,h'(x)>0,h(x)在R上为增函数,不满足有两个零点,故不合题意;
所以a>0,令h'(x)=0,解得x=lna,
并且有x∈(﹣∞,lna),h'(x)<0;x∈(lna,+∞),h'(x)>0,
故 ![]() .
.
(Ⅱ)证明:要证f(x0)<a<y0成立,
即证 ![]() ,不妨设x2>x1 ,
,不妨设x2>x1 ,
只需证 ![]() ,
,
即为 ![]() ,
,
要证 ![]() ,只需证
,只需证 ![]() ,
,
令 ![]() ,
,
只需证F(t)>0,求导 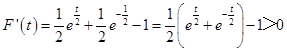 ,
,
∴F(t)在(0,+∞)为增函数,
故F(t)>F(0)=0,
∴ ![]() ;
;
要证 ![]() ,
,
只需证明 ![]() ,
,
令 ![]() ,
,
求导 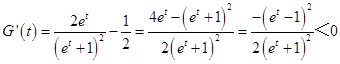 ,
,
∴G(t)在(0,+∞)为减函数,故G(t)<G(0)=0,
∴ ![]() ;
;
∴ ![]() ,t>0,成立,
,t>0,成立,
∴f(x0)<a<y0成立
【解析】(Ⅰ)先求导,利用导数求出函数最小值即可, (Ⅱ)利用分析法,要证f(x0)<a<y0 , 只需证 ![]() ,构造函数
,构造函数 ![]() ,利用导数只需证明
,利用导数只需证明 ![]() ,再构造函数,根据导数和函数的单调性的关系即可证明
,再构造函数,根据导数和函数的单调性的关系即可证明
【考点精析】利用函数的最值及其几何意义对题目进行判断即可得到答案,需要熟知利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在各项均为正数的等比数列{an}中,a1=2,且2a1 , a3 , 3a2成等差数列.
(Ⅰ) 求等比数列{an}的通项公式;
(Ⅱ) 若数列{bn}满足bn=11﹣2log2an , 求数列{bn}的前n项和Tn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C的坐标分别为(﹣ ![]() ,0),(
,0),( ![]() ,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心. 
(1)写出重心G的坐标;
(2)求外心O′,垂心H的坐标;
(3)求证:G,H,O′三点共线,且满足|GH|=2|OG′|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是东西方向的公路北侧的边缘线,某公司准备在
是东西方向的公路北侧的边缘线,某公司准备在![]() 上的一点
上的一点![]() 的正北方向的
的正北方向的![]() 处建设一仓库,设
处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站
的正方形无顶中转站![]() (其中
(其中![]() 在
在![]() 上),现从仓库
上),现从仓库![]() 向
向![]() 和中转站分别修两条道路
和中转站分别修两条道路![]() ,已知
,已知![]() ,且
,且![]() .
.

(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元![]() ,两条道路造价为30万元
,两条道路造价为30万元![]() ,问:
,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价
取何值时,该公司建设中转站围墙和两条道路总造价![]() 最低.
最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面命题正确的是( )
A.“![]() ”是“
”是“![]() ”的 充 分不 必 要条件
”的 充 分不 必 要条件
B.命题“若![]() ,则
,则![]() ”的 否 定 是“ 存 在
”的 否 定 是“ 存 在![]() ,则
,则![]() ”.
”.
C.设![]() ,则“
,则“![]() 且
且![]() ”是“
”是“![]() ”的必要而不充分条件
”的必要而不充分条件
D.设![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要 不 充 分 条件
”的必要 不 充 分 条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线y=x2-2x—3与两条坐标轴的三个交点都在圆C上.若圆C与直线x-y+a=0交于A,B两点,
(1)求圆C的标准方程;
(2)若 ![]() (O为原点),求a的值.
(O为原点),求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com