
【题目】正方体ABCD﹣A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,记B1与F的轨迹构成的平面为α.
①F,使得B1F⊥CD1
②直线B1F与直线BC所成角的正切值的取值范围是[![]() ,
,![]() ]
]
③α与平面CDD1C1所成锐二面角的正切值为2![]()
④正方体ABCD﹣A1B1C1D1的各个侧面中,与α所成的锐二面角相等的侧面共四个.
其中正确命题的序号是_____.(写出所有正确的命题序号)
【答案】①②③④
【解析】
分别取CC1和C1D1的中点为M,N,连接MN、MB1、NB1,然后利用面面平行的判定定理证明平面MNB1∥平面A1BE,从而确定平面MNB1就是平面α.
当F为线段MN的中点时,可证明①;
②利用平移的思想,将直线B1F与直线BC所成角转化为B1F与B1C1所成的角,由于B1C1⊥平面MNC1,所以tan∠FB1C1即为所求,进而求解即可;
③平面MNB1与平面CDD1C1所成的锐二面角即为所求,也就是求出tan∠B1QC1即可;
④由正方体的对称性和二面角的含义即可判断.
解:如图所示,

设正方体的棱长为2,分别取CC1和C1D1的中点为M,N,连接MN、MB1、NB1,则MN∥A1B,MB1∥EA1,
∵MN、MB1平面MNB1,A1B、EA1平面A1BE,且MN∩MB1=M,A1B∩EA1=A1,
∴平面MNB1∥平面A1BE,
∴当F在MN上运动时,始终有B1F∥平面A1BE,即平面MNB1就是平面α.
对于①,当F为线段MN的中点时,∵MB1=NB1,∴B1F⊥MN,∵MN∥CD1,∴B1F⊥CD1,即①正确;
对于②,∵BC∥B1C1,∴直线B1F与直线B1C1所成的角即为所求,
∵B1C1⊥平面MNC1,C1F平面MNC1,∴B1C1⊥C1F,
∴直线B1F与直线B1C1所成的角为∠FB1C1,且tan∠FB1C1![]() ,
,
而FC1的取值范围为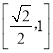 ,B1C1=2,所以tan∠FB1C1∈[
,B1C1=2,所以tan∠FB1C1∈[![]() ,
,![]() ],即②正确;
],即②正确;
对于③,平面MNB1与平面CDD1C1所成的锐二面角即为所求,
取MN的中点Q,因为B1C1⊥平面MNC1,所以∠B1QC1就是所求角,
而tan∠B1QC1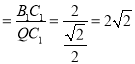 ,即③正确;
,即③正确;
对于④,由对称性可知,与α所成的锐二面角相等的面有平面BCC1B1,平面ADD1A1,平面A1B1C1D1,平面ABCD,即④正确.
故答案为:①②③④.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,焦距为2,抛物线
,焦距为2,抛物线![]() 的准线经过C的左焦点F.
的准线经过C的左焦点F.
(1)求C与M的方程;
(2)直线l经过C的上顶点且l与M交于P,Q两点,直线FP,FQ与M分别交于点D(异于点P),E(异于点Q),证明:直线DE的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约公元222年,赵爽为《周碑算经》一书作序时,介绍了“勾股圆方图”,又称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由3个全等的三角形与中间的一个小正三角形组成的一个大正三角形,设![]() ,若在大正三角形中随机取一点,则此点取自小正三角形的概率为( )
,若在大正三角形中随机取一点,则此点取自小正三角形的概率为( )
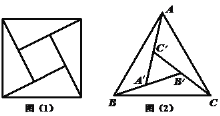
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线l的参数方程;
的直角坐标方程与直线l的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】配件厂计划为某项工程生产一种配件,这种配件每天的需求量是200件.由于生产这种配件时其他生产设备必须停机,并且每次生产时都需要花费5000元的准备费,所以需要周期性生产这种配件,即在一天内生产出这种配件,以满足从这天起连续n天的需求,称n为生产周期(假设这种配件每天产能可以足够大).配件的存储费为每件每天2元(当天生产出的配件不需要支付存储费,从第二天开始付存储费).在长期的生产活动中,为使每个生产周期内每天平均的总费用最少,那么生产周期n为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)写出曲线C1和C2的直角坐标方程;
(2)已知P为曲线C2上的动点,过点P作曲线C1的切线,切点为A,求|PA|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用![]() 代表红球,
代表红球,![]() 代表蓝球,
代表蓝球,![]() 代表黑球,由加法原理及乘法原理,从1个红球和1个蓝球中取出若干个球的所有取法可由
代表黑球,由加法原理及乘法原理,从1个红球和1个蓝球中取出若干个球的所有取法可由![]() 的展开式
的展开式![]() 表示出来,如:“1”表示一个球都不取、“
表示出来,如:“1”表示一个球都不取、“![]() ”表示取出一个红球,而“
”表示取出一个红球,而“![]() ”用表示把红球和蓝球都取出来.以此类推,下列各式中,其展开式可用来表示从5个有区别的红球、5个无区别的蓝球、5个无区别的黑球中取出若干个球,且所有的蓝球都取出或都不取出的所有取法的是( )
”用表示把红球和蓝球都取出来.以此类推,下列各式中,其展开式可用来表示从5个有区别的红球、5个无区别的蓝球、5个无区别的黑球中取出若干个球,且所有的蓝球都取出或都不取出的所有取法的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com