
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对40名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝![]() 以上为“常喝”,体重超过
以上为“常喝”,体重超过![]() 为“肥胖”.已知在全部40人中随机抽取1人,抽到肥胖学生的概率为
为“肥胖”.已知在全部40人中随机抽取1人,抽到肥胖学生的概率为![]() .
.
常喝 | 不常喝 | 合计 | |
肥胖 | 3 | ||
不肥胖 | 5 | ||
合计 | 40 |
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由.
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由.
参考公式:
①卡方统计量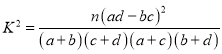 ,其中
,其中![]() 为样本容量;
为样本容量;
②独立性检验中![]() 的临界值参考表:
的临界值参考表:
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
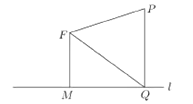
【题目】如图,平面上定点![]() 到定直线
到定直线![]() 的距离
的距离![]() ,
,![]() 为该平面上的动点,过
为该平面上的动点,过![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且
,且![]() ;
;
(1)试建立适当的平面直角坐标系,求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() 、
、![]() 两点,交直线
两点,交直线![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c.满足2acosC+bcosC+ccosB=0.
(Ⅰ)求角C的大小;
(Ⅱ)若a=2,△ABC的面积为![]() ,求C的大小。
,求C的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且2cos2![]() ·cosB-sin(A-B)sinB+cos(A+C)=-
·cosB-sin(A-B)sinB+cos(A+C)=-![]() .
.
(1)求cos A的值;
(2)若a=4![]() ,b=5,求
,b=5,求![]() 在
在![]() 方向上的投影.
方向上的投影.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为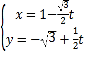 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场使用网箱养殖的方法,收获时随机抽取了 100个网箱,测量各箱水产品的产量(单位:![]() ),其产量都属于区间
),其产量都属于区间![]() ,按如下形式分成5组,第一组:
,按如下形式分成5组,第一组:![]() ,第二组:
,第二组:![]() ,第三组:
,第三组:![]() ,第四组:
,第四组:![]() ,第五组:
,第五组:![]() ,得到频率分布直方图如图:
,得到频率分布直方图如图:
定义箱产量在![]() (单位:
(单位:![]() )的网箱为“低产网箱”, 箱产量在区间
)的网箱为“低产网箱”, 箱产量在区间![]() 的网箱为“高产网箱”.
的网箱为“高产网箱”.

(1)若同一组中的每个数据可用该组区间的中点值代替,试计算样本中的100个网箱的产量的平均数;
(2)按照分层抽样的方法,从这100个样本中抽取25个网箱,试计算各组中抽取的网箱数;
(3)若在(2)抽取到的“低产网箱”及“高产网箱”中再抽取2箱,记其产量分别![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩.
某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布N(60,169).
(Ⅰ)求物理原始成绩在区间(47,86)的人数;
(Ⅱ)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com