
【题目】![]() 为椭圆
为椭圆![]() 上的点,
上的点,![]() 是两焦点,若
是两焦点,若![]() ,则
,则![]() 的面积是( )
的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
由题意得,在△F1PF2中,∠F1PF2=60°,|F1P|+|PF2|=![]() =
=![]() ,|F1F2|=4,利用余弦定理可求得|F1P||PF2|的值,从而可求得△PF1F2的面积.
,|F1F2|=4,利用余弦定理可求得|F1P||PF2|的值,从而可求得△PF1F2的面积.
∵椭圆![]() ,∴
,∴![]() =
=![]() ,b=2,c=2.又∵P为椭圆上一点,∠F1PF2=60°,
,b=2,c=2.又∵P为椭圆上一点,∠F1PF2=60°,
且F1、F2为左右焦点,由椭圆的定义得|F1P|+|PF2|=![]() =
=![]() ,|F1F2|=4,
,|F1F2|=4,
∴|F1F2|2=|PF1|![]() +|PF2|
+|PF2|![]() -2|PF1||PF2|cos60°
-2|PF1||PF2|cos60°
=(|PF1|+|PF2|)2﹣2|PF1||PF2|﹣2|F1P||PF2|cos60°
=32﹣3|F1P||PF2|
=16
∴|F1P||PF2|=![]() ,∴
,∴![]() =
=![]() |PF1||PF2|sin60°=
|PF1||PF2|sin60°=![]() ×
×![]() ×
×![]() =
=![]() .
.
故选:A.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】市场份额又称市场占有率,它在很大程度上反映了企业的竞争地位和盈利能力,是企业非常重视的一个指标.近年来,服务机器人与工业机器人以迅猛的增速占领了中国机器人领域庞大的市场份额,随着“一带一路”的积极推动,包括机器人产业在内的众多行业得到了更广阔的的发展空间,某市场研究人员为了了解某机器人制造企业的经营状况,对该机器人制造企业2017年1月至6月的市场份额进行了调查,得到如下资料:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
市场份额 | 11 | 163 | 16 | 15 | 20 | 21 |
请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程,并预测该企业2017年7月份的市场份额.
的线性回归方程,并预测该企业2017年7月份的市场份额.
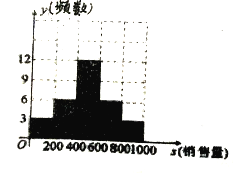
如图是该机器人制造企业记录的2017年6月1日至6月30日之间的产品销售频数(单位:天)统计图.设销售产品数量为![]() ,经统计,当
,经统计,当![]() 时,企业每天亏损约为200万元;
时,企业每天亏损约为200万元;
当![]() 时,企业平均每天收入约为400万元;
时,企业平均每天收入约为400万元;
当![]() 时,企业平均每天收入约为700万元.
时,企业平均每天收入约为700万元.
①设该企业在六月份每天收入为![]() ,求
,求![]() 的数学期望;
的数学期望;
②如果将频率视为概率,求该企业在未来连续三天总收入不低于1200万元的概率.
附:回归直线的方程是![]() ,其中
,其中
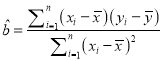 ,
, ![]() ,
,
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() 为下述条件的函数
为下述条件的函数![]() 的集合:①定义域为
的集合:①定义域为![]() ;②对任意实数
;②对任意实数![]() ,都有
,都有![]() .
.
(1)判断函数![]() 是否为
是否为![]() 中元素,并说明理由;
中元素,并说明理由;
(2)若函数![]() 是奇函数,证明:
是奇函数,证明:![]() ;
;
(3)设![]() 和
和![]() 都是
都是![]() 中的元素,求证:
中的元素,求证: 也是
也是![]() 中的元素,并举例说明,
中的元素,并举例说明, 不一定是
不一定是![]() 中的元素.
中的元素.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 过坐标原点
过坐标原点![]() 且圆心在曲线
且圆心在曲线![]() 上.
上.
(1)若圆![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() (不同于原点
(不同于原点![]() ),求证:
),求证:![]() 的面积为定值;
的面积为定值;
(2)设直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() ,求圆
,求圆![]() 的方程;
的方程;
(3)点![]() 在直线
在直线![]() 上,过点
上,过点![]() 引圆
引圆![]() (题(2))的两条切线
(题(2))的两条切线![]() ,切点为
,切点为![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】无穷数列![]()
![]() ,若存在正整数
,若存在正整数![]() ,使得该数列由
,使得该数列由![]() 个互不相同的实数组成,且对于任意的正整数
个互不相同的实数组成,且对于任意的正整数![]() ,
,![]() 中至少有一个等于
中至少有一个等于![]() ,则称数列
,则称数列![]() 具有性质
具有性质![]() .集合
.集合![]() .
.
(1)若![]() ,
,![]() ,判断数列
,判断数列![]() 是否具有性质
是否具有性质![]() ;
;
(2)数列![]() 具有性质
具有性质![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)数列![]() 具有性质
具有性质![]() ,对于
,对于![]() 中的任意元素
中的任意元素![]() ,
,![]() 为第
为第![]() 个满足
个满足![]() 的项,记
的项,记![]()
![]() ,证明:“数列
,证明:“数列![]() 具有性质
具有性质![]() ”的充要条件为“数列
”的充要条件为“数列![]() 是周期为
是周期为![]() 的周期数列,且每个周期均包含
的周期数列,且每个周期均包含![]() 个不同实数”.
个不同实数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 、
、![]() 为常数且
为常数且![]() ),满足条件
),满足条件![]() ,且方程
,且方程![]() 有等根.
有等根.
(1)若![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,
,![]() ,使
,使![]() 当定义域为
当定义域为![]() 时,值域为
时,值域为![]() ?如果存在,求出
?如果存在,求出![]() ,
,![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于往届高三年级数学学科的学习方式大都是“刷题一讲题一再刷题”的模式,效果不理想,某市一中的数学课堂教改采用了“记题型一刷题一检测效果”的模式,并记录了某学生的记题型时间![]() (单位:
(单位:![]() )与检测效果
)与检测效果![]() 的数据如下表所示.
的数据如下表所示.
记题型时间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
检测效果 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)据统计表明,![]() 与
与![]() 之间具有线性相关关系,请用相关系数
之间具有线性相关关系,请用相关系数![]() 加以说明(若
加以说明(若![]() ,则认为
,则认为![]() 与
与![]() 有很强的线性相关关系,否则认为没有很强的线性相关关系);
有很强的线性相关关系,否则认为没有很强的线性相关关系);
(2)建立![]() 关于
关于![]() 的回归方程,并预测该学生记题型
的回归方程,并预测该学生记题型的检测效果;
(3)在该学生检测效果不低于3.6的数据中任取2个,求检测效果均高于4.4的概率.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,
![]() ,相关系数
,相关系数
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com