
【题目】已知函数f(x)=x3﹣3ax(a∈R)
(1)当a=1时,求f(x)的极小值;
(2)若直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,求a的取值范围;
【答案】解:(1)∵当a=1时,f′(x)=3x2﹣3,令f′(x)=0,得x=﹣1或x=1,当f′(x)<0,即x∈(﹣1,1)时,f(x)为减函数;当f′(x)>0,即x∈(﹣∞,﹣1],或x∈[1,+∞)时,f(x)为增函数.∴f(x)在(﹣1,1)上单调递减,在(﹣∞,﹣1],[1,+∞)上单调递增∴f(x)的极小值是f(1)=﹣2
(2)∵f′(x)=3x2﹣3a≥﹣3a,∴要使直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,当且仅当﹣1<﹣3a时成立,∴![]()
【解析】(1)由f(x)=x3﹣3ax,得f′(x)=3x2﹣3a,当f′(x)>0,f′(x)<0时,分别得到f(x)的单调递增区间、单调递减区间,由此可以得到极小值为f(1)=﹣2.
(2)要使直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,只需令直线的斜率﹣1小于f(x)的切线的最小值即可,也就是﹣1<﹣3a.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某中学共有5000人,其中男生3500人,女生1500人,为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如下:
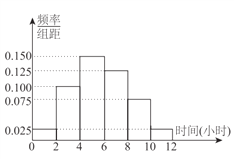
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中,有60位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理,我们( )
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别无关”
的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() 是实数常数,
是实数常数,![]() ).
).
(1)若![]() ,函数
,函数![]() 的图象关于点
的图象关于点![]() 成中心对称,求
成中心对称,求![]() ,
,![]() 的值;
的值;
(2)若函数![]() 满足条件(1),且对任意
满足条件(1),且对任意![]() ,总有
,总有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() 是奇函数,
是奇函数,![]() ,
,![]() ,且对任意
,且对任意![]() 时,不等式
时,不等式![]() 恒成立,求负实数
恒成立,求负实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数y=sin(2x+![]() )的图象向右平移
)的图象向右平移![]() 个单位,再把所得图象上各点的横坐标缩短到原来的
个单位,再把所得图象上各点的横坐标缩短到原来的![]() , 则所得图象的函数解析式是( )
, 则所得图象的函数解析式是( )
A.y=sin(4x+![]() π)
π)
B.y=sin(4x+![]() )
)
C.y=sin4x
D.y=sinx
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,则下列说法正确的是( ).
的图象,则下列说法正确的是( ).
A. ![]() B. 直线
B. 直线![]() 是
是![]() 的图象的一条对称轴
的图象的一条对称轴
C. ![]() 的最小正周期为
的最小正周期为![]() D.
D. ![]() 为奇函数
为奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇响应“绿水青山就是金山银山”的号召,因地制宜的将该镇打造成“生态水果特色小镇”.经调研发现:某珍稀水果树的单株产量![]() (单位:千克)与施用肥料
(单位:千克)与施用肥料![]() (单位:千克)满足如下关系:
(单位:千克)满足如下关系: ,肥料成本投入为
,肥料成本投入为![]() 元,其它成本投入(如培育管理、施肥等人工费)
元,其它成本投入(如培育管理、施肥等人工费)![]() 元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为
元.已知这种水果的市场售价大约为15元/千克,且销路畅通供不应求.记该水果树的单株利润为![]() (单位:元).
(单位:元).
(Ⅰ)求![]() 的函数关系式;
的函数关系式;
(Ⅱ)当施用肥料为多少千克时,该水果树的单株利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高一新生分成水平相同的甲、乙两个平行班,每班50人,某教师采用![]() 、
、![]() 两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.
两种不同的教学模式分别在甲、乙两个班进行教改实验,为了了解教学效果,期末考试后,该教师分别从两班中各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示,记成绩不低于90分为“成绩优秀”.

(1)在乙班的20个个体中,从不低于86分的成绩中随机抽取2人,求抽出的两个人均“成绩优秀”的概率;
(2)由以上统计数据填写![]() 列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
列联表;能否在犯错误的概率不超过0.10的前提下认为成绩优秀与教学模型有关.
甲班( | 乙班( | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.847 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立y关于t的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com