
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.
(1)三棱锥E—PAD的体积
V=PA·S△ADE=PA·=.
(2)当点E为BC的中点时,EF与平面PAC平行.
∵在△PBC中,E、F分别为BC、PB的中点,
∴EF∥PC,又EF⊄平面PAC,而PC⊂平面PAC,
∴EF∥平面PAC.
(3)证明:∵PA⊥平面ABCD,BE⊂平面ABCD,
∴EB⊥PA,
又EB⊥AB,AB∩AP=A,AB,AP⊂平面PAB,
∴EB⊥平面PAB,又AF⊂平面PAB,∴AF⊥EB,
又PA=AB=1,点F是PB中点,
∴AF⊥PB又∵PB∩BE=B,
PB,BE⊂面PBE,
∴AF⊥面PBE,
∵PE⊂面PBE,∴PE⊥AF.
【解析】略


科目:高中数学 来源:2012-2013学年湖南省株洲市高三第五次月考文科数学试卷(解析版) 题型:选择题
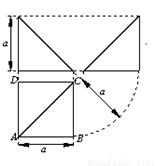
四棱锥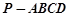 的三视图如右图所示,其中
的三视图如右图所示,其中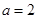 ,四棱锥
,四棱锥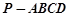 的五个顶点都在一个球面上,则该球表面积为( )
的五个顶点都在一个球面上,则该球表面积为( )
A.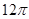 B.
B.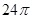 C.
C.
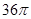 D.
D.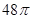
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
四棱锥 的三视图如右图所示,四棱锥
的三视图如右图所示,四棱锥 的五个顶点都在一个球面上,
的五个顶点都在一个球面上,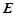 、
、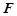 分别是棱
分别是棱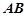 、
、 的中点,直线
的中点,直线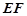 被球面所截得的线段长为
被球面所截得的线段长为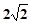 ,则该球表面积为 .
,则该球表面积为 .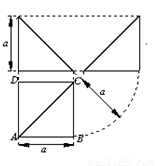
查看答案和解析>>
科目:高中数学 来源:2011-2012学年海南省高三高考极限压轴卷理科数学试卷(解析版) 题型:填空题
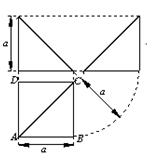
四棱锥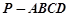 的三视图如右图所示,四棱锥
的三视图如右图所示,四棱锥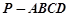 的五个顶点都在一个球面上,
的五个顶点都在一个球面上,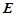 、
、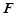 分别是棱
分别是棱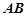 、
、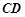 的中点,直线
的中点,直线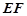 被球面所截得的线段长为
被球面所截得的线段长为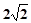 ,则该球表面积为 .
,则该球表面积为 .
查看答案和解析>>
科目:高中数学 来源:新课标高三数学空间图形的基本关系与公理、空间图形的平行关系专项训练(河北) 题型:解答题
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.
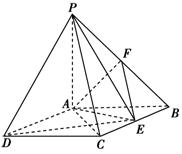 (1)求三棱锥E—PAD的体积;
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com