
【题目】某厂生产的某种零件的尺寸![]() 大致服从正态分布
大致服从正态分布![]() ,且规定尺寸
,且规定尺寸![]() 为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
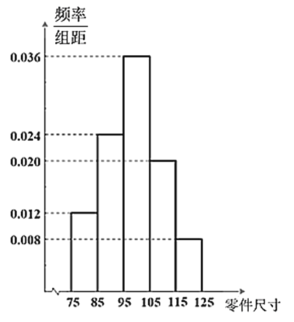
(1)估计生产线生产的零件的次品率及零件的平均尺寸;
(2)从生产线上随机取一箱零件,求这箱零件销售后的期望利润及不亏损的概率.
【答案】(1)0.20;98.8(2)![]()
【解析】
(1)求出![]() 的值,即可得到次品的尺寸范围,根据频率分布图求出次品率,并求出各组的频率,按照平均数公式即可求解;
的值,即可得到次品的尺寸范围,根据频率分布图求出次品率,并求出各组的频率,按照平均数公式即可求解;
(2)设生产线上的一箱零件(5件)中的正品数为![]() ,则
,则![]() ,将利润表示为
,将利润表示为![]() 的函数,由二项分布的期望公式和期望的性质,求出利润的期望;要使销售不亏损,5件产品中至少要有4件正品,根据独立重复试验的概率公式,即可求解.
的函数,由二项分布的期望公式和期望的性质,求出利润的期望;要使销售不亏损,5件产品中至少要有4件正品,根据独立重复试验的概率公式,即可求解.
(1)次品的尺寸范围![]() ,
,
即![]() ,即
,即![]() ,
,
故生产线生产的产品次品率为:![]()
生产线生产的产品平均尺寸为:
![]()
(2)设生产线上的一箱零件(5件)中的正品数为![]() ,
,
正品率为![]() ,故
,故![]() ,
,![]()
设销售生产线上的一箱零件获利为![]() 元,
元,
则![]()
![]() (元)
(元)
设事件![]() :销售生产线上的一箱零件不亏损,则
:销售生产线上的一箱零件不亏损,则
![]()
![]() ,
,
答:生产线生产的零件的次品率为0.2,零件的平均尺寸为98.8,
这箱零件销售后的期望利润为100元,不亏损的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进![]() 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式;
)的函数解析式;
(2)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天的各需求量的频率作为各需求量发生的概率.
天的各需求量的频率作为各需求量发生的概率.
![]() 若花店一天购进
若花店一天购进![]() 枝玫瑰花,
枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列, 数学期望及方差;
的分布列, 数学期望及方差;
![]() 若花店一天购进
若花店一天购进![]() 枝或
枝或![]() 枝玫瑰花,你认为应购进
枝玫瑰花,你认为应购进![]() 枝还是
枝还是![]() 枝?请说明理由.
枝?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.

(1)求证:当点F,A,D不共线时,线段MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,线段MN总与线段FD平行”这个结论正确吗?如果正确,请证明;如果不正确,请说明能否改变个别已知条件使上述结论成立,并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,设实数
,设实数![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 满足
满足
(i)![]() 、
、![]() 、
、![]() 且不全为0;
且不全为0;
(ii)![]() 、
、![]() 、
、![]() ;
;
(iii)若![]() ,则
,则![]() .
.
若所有形如![]() 和
和![]() 的数均不为2014的倍数,则称集合
的数均不为2014的倍数,则称集合![]() 为“好集”.求好集
为“好集”.求好集![]() 所含元素个数的最大值.
所含元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四面体![]() 的各棱长均为2,
的各棱长均为2,![]() 、
、![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 、
、![]() 的中点,以
的中点,以![]() 为圆心、1为半径,分别在面
为圆心、1为半径,分别在面![]() 、面
、面![]() 内作弧
内作弧![]() ,并将两弧各分成五等份,分点顺次为
,并将两弧各分成五等份,分点顺次为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 以及
以及![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .一只甲虫欲从点
.一只甲虫欲从点![]() 出发,沿四面体表面爬行至点
出发,沿四面体表面爬行至点![]() ,则其爬行的最短距离为___________。
,则其爬行的最短距离为___________。
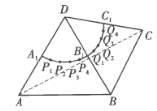
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园内有一块以![]() 为圆心半径为
为圆心半径为![]() 米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形
米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形![]() 区域,其中两个端点
区域,其中两个端点![]() ,
,![]() 分别在圆周上;观众席为梯形
分别在圆周上;观众席为梯形![]() 内切在圆
内切在圆![]() 外的区域,其中
外的区域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在点
在点![]() 的同侧.为保证视听效果,要求观众席内每一个观众到舞台
的同侧.为保证视听效果,要求观众席内每一个观众到舞台![]() 处的距离都不超过
处的距离都不超过![]() 米.设
米.设![]() ,
,![]() .问:对于任意
.问:对于任意![]() ,上述设计方案是否均能符合要求?
,上述设计方案是否均能符合要求?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com