
【题目】设z1 , z2是复数,则下列命题中的假命题是( )
A.若|z1﹣z2|=0,则 ![]() =
= ![]()
B.若z1= ![]() ,则
,则 ![]() =z2
=z2
C.若|z1|=|z2|,则z1? ![]() =z2?
=z2? ![]()
D.若|z1|=|z2|,则z12=z22
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】网上购物系统是一种具有交互功能的商业信息系统,它在网络上建立一个虚拟的购物商场,使购物过程变得轻松、快捷、方便.网上购物系统分为前台管理和后台管理,前台管理包括浏览商品、查询商品、订购商品、用户注册等功能;后台管理包括公告管理、商品管理、订单管理、投诉管理和用户管理等模块.根据这些要求画出该系统的结构图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆C的方程为ρ=2acosθ(a≠0),以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为 ![]() (t为参数).
(t为参数).
(1)求圆C的直角坐标方程(化为标准方程)和直线l的极坐标方程;
(2)若直线l与圆C只有一个公共点,且a<1,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,且AB=AD,BC=DC.
(1)求证:![]() ∥平面EFGH;
∥平面EFGH;
(2)求证:四边形EFGH是矩形.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(1,﹣1),B(4,0),C(2,2),平面区域D是所有满足 ![]() =
= ![]() +μ
+μ ![]() (1<λ≤a,1<μ≤b)的点P(x,y)组成的区域.若区域D的面积为8,则4a+b的最小值为 ( )
(1<λ≤a,1<μ≤b)的点P(x,y)组成的区域.若区域D的面积为8,则4a+b的最小值为 ( )
A.5
B.4 ![]()
C.9
D.5+4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是直角△ABC斜边BC上一点,AC= ![]() DC.
DC.
(I)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD=2 ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产一种品牌服装的年固定成本为10万元,且每生产1万件,需要另投入1.9万元.设R(x)(单位:万元)为销售收入,根据市场调查知R(x)= 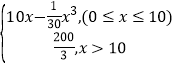 其中x(单位:万件)是年产量.
其中x(单位:万件)是年产量.
(1)写出年利润W(单位:万元)关于年产量x的函数解析式.
(2)当年产量为多少时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com