
 .
.

 表示函数f(x)在区间[0,6]上与x轴所围成的图形的面积,
表示函数f(x)在区间[0,6]上与x轴所围成的图形的面积, +
+ =
= +
+ ,故④错误.
,故④错误.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
 如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•江门二模)将边长为2的等边三角形PAB沿x轴滚动,某时刻P与坐标原点重合(如图),设顶点P(x,y)的轨迹方程是y=f(x),关于函数y=f(x)的有下列说法:
(2013•江门二模)将边长为2的等边三角形PAB沿x轴滚动,某时刻P与坐标原点重合(如图),设顶点P(x,y)的轨迹方程是y=f(x),关于函数y=f(x)的有下列说法:| ∫ | 6 0 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省五校高三下学期第二次联考理科数学试卷(解析版) 题型:解答题
已知直角梯形 中,
中, 是边长为2的等边三角形,
是边长为2的等边三角形, .沿
.沿 将
将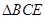 折起,使
折起,使 至
至 处,且
处,且 ;然后再将
;然后再将 沿
沿 折起,使
折起,使 至
至 处,且面
处,且面 面
面 ,
, 和
和 在面
在面 的同侧.
的同侧.


(Ⅰ) 求证: 平面
平面 ;
;
(Ⅱ) 求平面 与平面
与平面 所构成的锐二面角的余弦值.
所构成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com