
分析 (1)由数列递推式:当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1,即可得到所求通项公式;
(2)求得bn=${log_2}{a_n}={log_2}{2^n}=n$,cn=an+bn=2n+n,运用数列的求和方法:分组求和,结合等比数列和等差数列的求和公式,即可得到所求和.
解答 解:(1)数列{an}的前n项和${S_n}={2^{n+1}}-2$,
当n=1时,a1=S1=2,
∴当n≥2时,Sn-1=2n-2,
∴an=Sn-Sn-1=(2n+1-2)-(2n-2)=2n,
当n=1时,成立,
∴数列{an}是以2为首项,以2为公比的等比数列,
∴数列{an}的通项公式为:an=2n;
(2)bn=${log_2}{a_n}={log_2}{2^n}=n$,
由cn=an+bn=2n+n,
数列{cn}的前n项和Tn=a1+b1+a2+b2+…+an+bn
=(2+22+23+…+2n)+(1+2+3+…+n)
=$\frac{2(1-{2}^{n})}{1-2}$+$\frac{(1+n)n}{2}$=2n+1-2+$\frac{(1+n)n}{2}$,
故数列{cn}的前n项和Tn=2n+1-2+$\frac{(1+n)n}{2}$.
点评 本题考查数列的通项公式的求法,注意运用数列递推式:当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1,考查数列的求和方法:分组求和,注意运用等差数列和等比数列的求和公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 5 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\stackrel{→}{AC}$ | B. | $\stackrel{→}{BD}$ | C. | $\stackrel{→}{CA}$ | D. | $\stackrel{→}{DB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知向量$\overrightarrow{AB}=({6,1}),\overrightarrow{BC}=({x,y}),\overrightarrow{CD}=({-2,-3})$.
如图,已知向量$\overrightarrow{AB}=({6,1}),\overrightarrow{BC}=({x,y}),\overrightarrow{CD}=({-2,-3})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
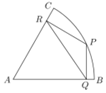 如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.
如图,扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条商业街道,要求街道PQ与AB垂直,街道PR与AC垂直,线段RQ表示第三条街道.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com