
【题目】三棱锥P﹣ABC中,已知PA=PB=PC=AC=4,BC= ![]() AB=2
AB=2 ![]() ,O为AC中点.
,O为AC中点. 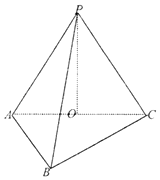
(1)求证:PO⊥平面ABC;
(2)求异面直线AB与PC所成角的余弦值.
【答案】
(1)证明:由题意,∵PA=PB=PC=AC=4,AC的中点O,
连接OP,OB,易得:OP⊥AC;
∵ ![]() ,
,
![]() ,
,
∴AC2=AB2+BC2,
故得△ABC为Rt△,
∴OB=OC=2,PB2=OB2+OP2,
∴OP⊥OB.
又∵AC∩BO=O且AC、OB面ABC,
∴OP⊥平面ABC
(2)解:分别取PB,BC中点EF,连接OE,OF,EF,
则AB∥OF,PC∥EF,故,∠EFO为异面直线AB与PC所成角(或补角)
由(Ⅰ)知在直角三角形POB中, ![]() ,
,
又 ![]() ,
, ![]() ;
;
在等腰三角形EOF中, ![]() .
.
所以,异面直线AB与PC所成角的余弦值为 ![]() .
.

【解析】(1)直线垂直平面,只需要证明直线垂直平面内的两条相交直线即可.由题意,因为PA=PB=PC=AC=4,AC的中点O,连接OP,OB,易得:OP⊥AC,同理可证△ABC为Rt△,OP⊥OB,AC∩BO=O且AC、OB面ABC可得OP⊥平面ABC.(2)利用O为AC中点,分别取PB,BC中点EF,连接OE,OF,EF,则AB∥OF,PC∥EF,故,∠EFO为异面直线AB与PC所成角.放在等腰三角形EOF即可求解.
【考点精析】认真审题,首先需要了解异面直线及其所成的角(异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系),还要掌握直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)的相关知识才是答题的关键.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】一大学生自主创业,拟生产并销售某电子产品![]() 万件(生产量与销售量相等),为扩大影响进行促销,促销费用
万件(生产量与销售量相等),为扩大影响进行促销,促销费用![]() (万元)满足
(万元)满足![]() (其中
(其中![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本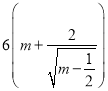 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 元/件.
元/件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,此大学生所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (p,q为常数)是定义在(﹣1,1)上的奇函数,且
(p,q为常数)是定义在(﹣1,1)上的奇函数,且 ![]() .
.
(1)求函数f(x)的解析式;
(2)判断并用定义证明f(x)在(﹣1,1)上的单调性;
(3)解关于x的不等式f(2x﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于在区间[a,b]上有意义的两个函数f(x)和g(x),如果对于任意x∈[a,b]均有|f(x)﹣g(x)|≤1成立,则称函数f(x)和g(x)在区间[a,b]上是接近的.若f(x)=log2(ax+1)与g(x)=log2x在区[1,2]上是接近的,则实数a的取值范围是( )
A.[0,1]
B.[2,3]
C.[0,2)
D.(1,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),若对任意x1∈R,都存在x2∈[﹣2,+∞),使得f(x1)>g(x2),则实数a的取值范围是( )
A.![]()
B.(0,+∞)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且满足不等式22a+1>25a﹣2 .
(1)求实数a的取值范围.
(2)求不等式loga(3x+1)<loga(7﹣5x).
(3)若函数y=loga(2x﹣1)在区间[1,3]有最小值为﹣2,求实数a值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件) | 产品B(件) | ||
研制成本、搭载费用之和(万元) | 20 | 30 | 计划最大资金额300万元 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题P:将函数sin2x的图象向右平移 ![]() 个单位得到函数y=sin(2x﹣
个单位得到函数y=sin(2x﹣ ![]() )的图象;命题Q:函数y=sin(x+
)的图象;命题Q:函数y=sin(x+ ![]() )cos(
)cos( ![]() ﹣x)的最小正周期是π,则复合命题“P或Q”“P且Q”“非P”为真命题的个数是个.
﹣x)的最小正周期是π,则复合命题“P或Q”“P且Q”“非P”为真命题的个数是个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com