
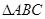 中,“
中,“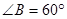 ”是
”是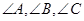 三个角成等差数列的充要条件;
三个角成等差数列的充要条件;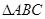 中,若
中,若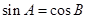 ,则
,则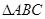 为直角三角形.
为直角三角形.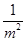 得,a<b,反之,若a<b,则取m2=0时不能得到am2<bm2,故am2<bm2是a<b的充分不必要条件,故命题②不正确.原命题:矩形的两条对角线相等.则其否命题为:若四边形不是矩形,则其对角线不相等.此否命题为假命题,如等腰梯形不是矩形,但其对角线相等,故命题③正确.在△ABC中,若∠B=60°,因为∠A+∠B+∠C=180°,得∠A+∠C=180°-∠B=180°-60°=120°,所以2∠B=∠A+∠C,所以∠A,∠B,∠C三个角成等差数列.若∠A,∠B,∠C三个角成等差数列,可设公差为d,则∠A=∠B-d,∠C=∠B+d,由∠A+∠B+∠C=180°,得∠B-d+∠B+∠b+d=180°,∴∠B=60°.所以在△ABC中,“∠B=60°”是∠A,∠B,∠C三个角成等差数列的充要条件,故命题④正确.在△ABC中,若sinA=cosB,则sinA=sin(90°-B),所以A=90°-B或A+90°-B=180°,所以A+B=90°或A-B=90°,则△ABC不一定为直角三角形,故命题⑤不正确.故答案为②⑤.
得,a<b,反之,若a<b,则取m2=0时不能得到am2<bm2,故am2<bm2是a<b的充分不必要条件,故命题②不正确.原命题:矩形的两条对角线相等.则其否命题为:若四边形不是矩形,则其对角线不相等.此否命题为假命题,如等腰梯形不是矩形,但其对角线相等,故命题③正确.在△ABC中,若∠B=60°,因为∠A+∠B+∠C=180°,得∠A+∠C=180°-∠B=180°-60°=120°,所以2∠B=∠A+∠C,所以∠A,∠B,∠C三个角成等差数列.若∠A,∠B,∠C三个角成等差数列,可设公差为d,则∠A=∠B-d,∠C=∠B+d,由∠A+∠B+∠C=180°,得∠B-d+∠B+∠b+d=180°,∴∠B=60°.所以在△ABC中,“∠B=60°”是∠A,∠B,∠C三个角成等差数列的充要条件,故命题④正确.在△ABC中,若sinA=cosB,则sinA=sin(90°-B),所以A=90°-B或A+90°-B=180°,所以A+B=90°或A-B=90°,则△ABC不一定为直角三角形,故命题⑤不正确.故答案为②⑤.

 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源:不详 题型:填空题
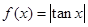 是周期为
是周期为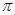 的偶函数;
的偶函数;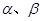 是第一象限的角,且
是第一象限的角,且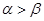 ,则
,则 ;
;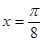 是函数
是函数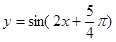 的一条对称轴方程;
的一条对称轴方程; 内方程
内方程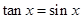 有3个解.
有3个解.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
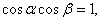 则
则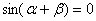 ;②已知直线
;②已知直线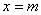 与函数
与函数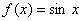 ,
,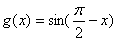 的图象分别交于
的图象分别交于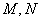 两点,则
两点,则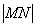 的最大值为
的最大值为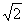 ;
;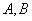 是△
是△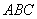 的两内角,如果
的两内角,如果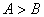 ,则
,则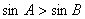 ;
;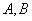 是锐角△
是锐角△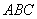 的两内角,则
的两内角,则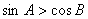 。
。| A.1 | B.2 | C.3 | D. 4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
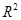 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;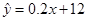 中,当解释变量
中,当解释变量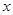 每增加一个单位时,预报变量
每增加一个单位时,预报变量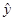 平均增加
平均增加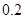 个单位;
个单位;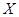 与
与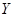 ,若它们的随机变量
,若它们的随机变量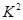 的观测值
的观测值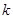 越小,则判断“
越小,则判断“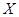 与
与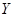 有关系”的把握程度越大.
有关系”的把握程度越大.| A.①④ | B.②④ | C.①③ | D.②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com