已知圆心为C的圆经过三个点O(0,0)、A(1,3)、B(4,0)
(1)求圆C的方程;
(2)求过点P(3,6)且被圆C截得弦长为4的直线的方程.
【答案】
分析:(1)设出圆的一般式方程,利用圆上的三点,即可求圆C的方程;
(2)通过过点P(3,6)且被圆C截得弦长为4的直线的斜率不存在推出方程判断是否满足题意;直线的斜率存在是利用圆心距与半径的关系,求出直线的斜率,即可解得直线的方程.
解答:解:(1)设圆的方程为x
2+y
2+Dx+Ey+F=0.
圆C经过三个点O(0,0)A(1,3)B(4,0),
所以
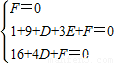
解得D=-4,E=-2,F=0,
所以圆C的方程x
2+y
2-4x-2y=0.
(2)①过点P(3,6)且被圆C截得弦长为4的直线的斜率不存在,此时x=3,满足题意.
②当过点P(3,6)且被圆C截得弦长为4的直线的斜率存在时设为k,
直线方程为y-6=k(x-3).
则
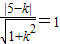
,解得k=
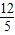
,所求直线方程为:12x-5y-6=0.
故所求直线方程为:x=3或12x-5y-6=0.
点评:本题考查圆的一般式方程的求法,直线与圆的位置关系的应用,考查计算能力.

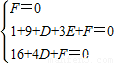
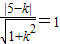 ,解得k=
,解得k=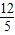 ,所求直线方程为:12x-5y-6=0.
,所求直线方程为:12x-5y-6=0.
