练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】函数f（x）= +lg（1+3x）的定义域是（ ）
    A.（﹣∞，﹣ ）?
    B.（﹣ ， ）∪（ ，+∞）?
    C.（ ，+∞）?
    D.（ ， ）∪（ ，+∞）

    【答案】B
    【解析】解：由1﹣2x≠0.1+3x＞0， 可得x＞﹣ ，且x≠ ，
    则定义域为（﹣ ， ）∪（ ，+∞），
    故选：B．
    【考点精析】通过灵活运用函数的定义域及其求法，掌握求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 （a＞0）．
    （1）证明：当x＞0时，f（x）在 上是减函数 ，在上是增函数，并写出当x＜0时f（x）的单调区间；
    （2）已知函数 ，函数g（x）=﹣x﹣2b，若对任意x1∈[1，3]，总存在x2∈[1，3]，使得g（x2）=h（x1）成立，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某房产开发商投资81万元建一座写字楼，第一年装修费为1万元，以后每年增加装修费2万元，现把写字楼出租，每年收入租金30万元．
    （1）若扣除投资和各种装修费，则从第几年开始获取纯利润？
    （2）若干年后开发商为了投资其他项目，有两种处理方案：
    ①年平均利润最大时，以50万元出售该楼；
    ②纯利润总和最大时，以10万元出售该楼；
    问选择哪种方案盈利更多？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|0＜ ≤1}，B={y|y=（ ）x ， 且x＜﹣1}
    （1）若集合C={x|x∈A∪B，且xA∩B}，求集合C；
    （2）设集合D={x|3﹣a＜x＜2a﹣1}，满足A∪D=A，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司每个工作日由位于市区的总公司向位于郊区的分公司开一个来回的班车（每年按200个工作日计算），现有两种使用班车的方案，方案一是购买一辆大巴，需花费90万元，报废期为10年，车辆平均每年的各种费用合计5万元，司机年工资6万元，司机每天请假的概率为0.1（每年请假时间不超过15天不扣工资，超过15天每天100元），若司机请假则需从公交公司雇佣司机，每天支付300元工资.方案二是租用公交公司的车辆（含司机），根据调研每年12个月的车辆需求指数如直方图所示，其中当某月车辆需求指数在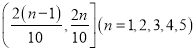时，月租金为万元.

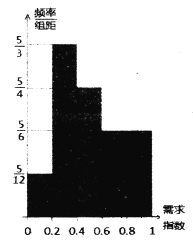
    （1）若购买大巴，设司机每年请假天数为，求公司因司机请假而增加的花费（元）及使用班车年平均花费（万元）的数学期望.

    （2）试用调研数据，给出公司使用班车的建议，使得年平均花费最少.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：关于x的不等式ax＞1，（a＞0，a≠1）的解集是{x|x＜0}，命题q：函数y=lg（x2﹣x+a）的定义域为R，若p∨q为真p∧q为假，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f（x）是R上的偶函数，对于任意x∈R，都有f（x+6）=f（x）+f（3）成立，当x1 ， x2∈[0，3]，且x1≠x2时，都有 ．给出下列命题： ①f（3）=0；
    ②直线x=﹣6是函数y=f（x）的图象的一条对称轴；
    ③函数y=f（x）在[﹣9，﹣6]上为增函数；
    ④函数y=f（x）在[﹣9，9]上有四个零点．
    其中所有正确命题的序号为（把所有正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】祖暅原理也就是“等积原理”，它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的，祖暅原理的内容是：夹在两个平行平面间的两个几何体，被平行于这两个平行平面的平面所截，如果截得两个截面的面积总相等，那么这两个几何体的体积相等．已知，两个平行平面间有三个几何体，分别是三棱锥、四棱锥、圆锥（高度都为），其中：三棱锥的底面是正三角形（边长为），四棱锥的底面是有一个角为的菱形（边长为），圆锥的体积为，现用平行于这两个平行平面的平面去截三个几何体，如果截得的三个截面的面积相等，那么，下列关系式正确的是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： =1（a＞b＞0）上的动点到焦点距离的最小值为 -1．以原点为圆心、椭圆的短半轴长为半径的圆与直线x﹣y+ =0相切．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若过点M（2，0）的直线与椭圆C相交于A，B两点，P为椭圆上一点，且满足 + =t （O为坐标原点）．当|AB|= 时，求实数t的值．

    查看答案和解析>>

    同步练习册答案