
��֪����{an}��a1��a��a2��p(����p��0)���������������n��Sn��a1��a2������an������Sn����![]() ��
��
(1)��a��ֵ��
(2)��ȷ������{an}�Ƿ��ǵȲ����У����ǣ������ͨ�ʽ�������ǣ�˵�����ɣ�
(3)��������{bn}���������һ������bʹ�ö������������n����bn��b����![]() �����bΪ����{bn}�ġ��Ͻ���ֵ������
�����bΪ����{bn}�ġ��Ͻ���ֵ������![]() ��������{p1��p2������pn��2n}�ġ��Ͻ���ֵ����
��������{p1��p2������pn��2n}�ġ��Ͻ���ֵ����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| n(an-a1) |
| 2 |
| Sn+2 |
| Sn+1 |
| Sn+1 |
| Sn+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| 5 |
| an |
| an+1 |
| 4an+2 |
| an+1+2 |
| 1 |
| an |
| 4 |
| 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| 5 |
| an |
| an+1 |
| 4an+2 |
| an+1+2 |
| 4 |
| 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| n(an-a1) |
| 2 |
| lim |
| n���� |
| an-1 |
| an+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������������ʦ����2009��2010ѧ���������ĩ���Ը߶���ѧ���⣨���ƣ� ���ͣ������
20�� (��������13��)
��֪����{an}��a1 = a��a2 = p������p > 0�����������������n��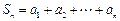 ����
����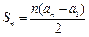 ��
��
(1)��a��ֵ��
(2)��ȷ������{an}�Ƿ��ǵȲ����У����ǣ������ͨ�ʽ�������ǣ�˵�����ɣ�
(3)��������{bn}���������һ������b��ʹ�ö������������n����bn< b����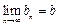 �����bΪ����{bn}�ġ��Ͻ���ֵ������
�����bΪ����{bn}�ġ��Ͻ���ֵ������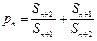 ��������
��������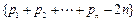 �ġ��Ͻ���ֵ����
�ġ��Ͻ���ֵ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com