
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() 且满足
且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)求出![]() ,分五种情况讨论
,分五种情况讨论![]() 的范围,分别令
的范围,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)由(1)可知,
的减区间;(2)由(1)可知,![]() ,不等式
,不等式![]() 化为
化为![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,利用导数研究函数的单调性,证明当
,利用导数研究函数的单调性,证明当![]() 时,不等式不成立,当
时,不等式不成立,当![]() 时,可证明
时,可证明![]() ,适量题意,即
,适量题意,即![]() .
.
试题解析:(1)定义域为![]() ,
,
![]() ,
,
当![]() 或
或![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
于是结合函数定义域的分析可得:
当![]() 时,函数
时,函数![]() 在定义域
在定义域![]() 上是增函数;
上是增函数;
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,此时有
,此时有![]() ,
,
于是![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,
,
于是![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,此时有
,此时有![]() ,
,
于是![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
当![]() 时,函数
时,函数![]() 定义域为
定义域为![]() ,
,
于是![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是增函数.
上是增函数.
(2)由(1)知![]() 存在两个极值点时,
存在两个极值点时,![]() 的取值范围是
的取值范围是![]() ,
,
由(1)可知,![]() ,
,
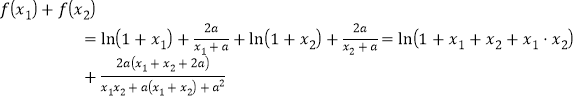
![]() ;
;
不等式![]() 化为
化为![]() ,
,
令![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() ,适量题意,即
,适量题意,即![]() .
.
综上,若![]() ,此时正数
,此时正数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】【2018届北京市海淀区】如图,三棱柱![]() 侧面
侧面![]() 底面
底面![]() ,
, ![]()
![]()
![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
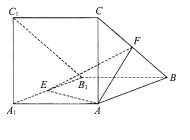
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求三棱柱![]() 的体积;
的体积;
(Ⅲ)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解户籍性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为100的调查样本,其中城镇户籍与农民户籍各50人;男性60人,女性40人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
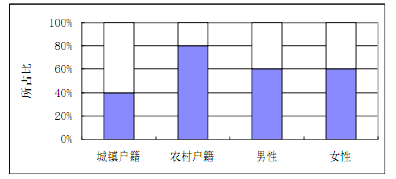
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别无关
C. 倾向选择生育二胎的人员中,男性人数与女性人数相同
D. 倾向选择生育二的人员中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地一商场记录了![]() 月份某
月份某![]() 天当中某商品的销售量
天当中某商品的销售量![]() (单位:
(单位:![]() )与该地当日最高气温
)与该地当日最高气温![]() (单位:
(单位:![]() )的相关数据,如下表:
)的相关数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)试求![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地
之间是正相关还是负相关;若该地![]() 月某日的最高气温是
月某日的最高气温是![]() ,试用所求回归方程预测这天该商品的销售量;
,试用所求回归方程预测这天该商品的销售量;
(3)假定该地![]() 月份的日最高气温
月份的日最高气温![]() ,其中
,其中![]() 近似取样本平均数
近似取样本平均数![]() ,
,![]() 近似取样本方差
近似取样本方差![]() ,试求
,试求![]() .
.
附:参考公式和有关数据 ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,且
,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一200名学生的期中考试语文成绩服从正态分布![]() ,数学成绩的频数分布直方图如下:
,数学成绩的频数分布直方图如下:

(1)计算这次考试的数学平均分,并比较语文和数学哪科的平均分较高(假设数学成绩在频率分布直方图中各段是均匀分布的);
(2)如果成绩大于85分的学生为优秀,这200名学生中本次考试语文、数学优秀的人数大约各多少人?
(3)如果语文和数学两科都优秀的共有4人,从(2)中的这些同学中随机抽取3人,设三人中两科都优秀的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附参考公式)若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来随着素质教育的不断推进,高考改革趋势明显.国家教育部先后出台了有关高考的《学业水平考试》、《综合素质评价》、《加分项目瘦身与自主招生》三个重磅文件,引起社会极大关注,有人说:男孩苦,女孩乐!为了了解某地区学生和包括老师,家长在内的社会人士对高考改革的看法,某媒体在该地区选择了![]() 人,,就是否“赞同改革”进行调查,调查统计的结果如下表:
人,,就是否“赞同改革”进行调查,调查统计的结果如下表:
赞同 | 不赞同 | 无所谓 | |
在校学生 |
|
|
|
社会人士 |
|
|
|
已知在全体样本中随机抽取![]() 人,抽到持“不赞同”态度的人的概率为
人,抽到持“不赞同”态度的人的概率为![]() .
.
(1)现用分层抽样的方法在所有参与调查的人中抽取![]() 人进行问卷访谈,文应该在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,文应该在持“无所谓”态度的人中抽取多少人?
(2)在持“不赞同”态度的人中,用分层抽样方法抽取![]() 人,若从
人,若从![]() 人中任抽
人中任抽![]() 人进一步深入调查,为更多了解学生的意愿,要求在校学生人数不少于社会人士人士,求恰好抽到两名在校学生的概率.
人进一步深入调查,为更多了解学生的意愿,要求在校学生人数不少于社会人士人士,求恰好抽到两名在校学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com