
【题目】将一颗均匀的骰子掷两次,第一次得到的点数记为![]() ,第一次得到的点数记为
,第一次得到的点数记为![]() ,则方程组
,则方程组![]() 有唯一解的概率是___________.
有唯一解的概率是___________.
【答案】![]()
【解析】
所有的可能的结果(a,b)共有6×6=36种,满足直线l1与l2平行的结果(a,b)共有3个,由此求得直线l1与l2平行的概率,用1减去直线l1与l2平行的概率,即得所求.
由题意可知,方程组有唯一解转化为表示方程组![]() 的两直线相交,
的两直线相交,
即直线l1:ax+by=3与直线l2:x+2y=2相交,
又所有的可能出现的结果(a,b)共有6×6=36种,当直线l1与l2平行时,应有![]() ,
,
故其中满足直线l1与直线l2平行的结果(a,b)共有:(1,2)、(2,4)、(3,6),总计3个,故直线l1与l2平行的概率为![]() .又由a,b的意义可知两条直线不重合,
.又由a,b的意义可知两条直线不重合,
故直线l1与l2相交的概率为 1![]() ,
,
∴方程组有唯一解的概率为 1![]() ,
,
故答案为:![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平
近似为样本平
均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)央视媒体平台从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.附:
的人数是Y,求变量Y的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解户籍性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为![]() 的调查样本,其中城镇户籍与农民户籍各
的调查样本,其中城镇户籍与农民户籍各![]() 人;男性
人;男性![]() 人,女性
人,女性![]() 人.绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
人.绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
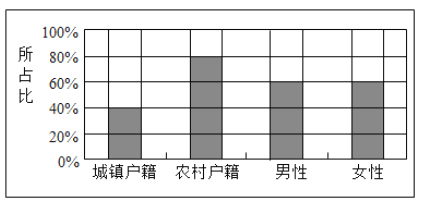
A.是否倾向选择生育二胎与户籍有关
B.是否倾向选择生育二胎与性别无关
C.倾向选择生育二胎的人员中,男性人数与女性人数相同
D.倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线![]() 的参数方程为
的参数方程为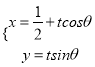 ,(
,( ![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() 是棱
是棱![]() 上的一点,满足
上的一点,满足![]() 平面
平面![]() .
.
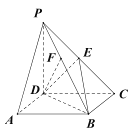
(Ⅰ)证明:![]() ;
;
(Ⅱ)设![]() ,
,![]() ,若
,若![]() 为棱
为棱![]() 上一点,使得直线
上一点,使得直线![]() 与平面
与平面![]() 所成角的大小为30°,求
所成角的大小为30°,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有两个国家AAAA级景区—甲景区和乙景区.相关部门统计了这两个景区2019年1月至6月的客流量(单位:百人),得到如图所示的茎叶图.关于2019年1月至6月这两个景区的客流量,下列结论正确的是( )
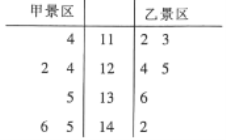
A.甲景区客流量的中位数为13000
B.乙景区客流量的中位数为13000
C.甲景区客流量的平均值比乙景区客流量的平均值小
D.甲景区客流量的极差比乙景区客流量的极差大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com