某种产品的广告费支出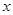
与销售额
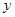（单位：百万元）之间有如下对应数据：
（1）画出散点图。
（2）求回归直线方程。
（3）试预测广告费支出为10百万元时，销售额多大
（1）建立直角坐标系，然后描点法来得到。
（2）
（3）82.5
解析试题分析：（2）由已知列出图表：
科目：高中数学
来源：
题型：解答题
在研究色盲与性别的关系调查中，调查了男性480人，其中有38人患色盲，调查的520个女性中6人患色盲，
科目：高中数学
来源：
题型：解答题
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表：
科目：高中数学
来源：
题型：解答题
在某次测验中，有6位同学的平均成绩为75分．用
科目：高中数学
来源：
题型：解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵树。乙组记录中有一个数据模糊，无法确认，在图中以X表示.
科目：高中数学
来源：
题型：解答题
我校某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题.
科目：高中数学
来源：
题型：解答题
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨
科目：高中数学
来源：
题型：解答题
（本小题满分12分）
科目：高中数学
来源：
题型：解答题
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
1 2 3 4 5 
2 4 5 6 8 
30 40 60 50 70 
60 160 300 300 560 
4 16 25
练习册系列答案
英才小状元系列答案
英才计划期末集中赢系列答案
银博士轻巧夺冠系列答案
一通百通考必赢系列答案
一线名师夺冠王检测卷系列答案
一路领先优选卷系列答案
一路领先口算题卡系列答案
一课3练课时导练系列答案
一飞冲天课时作业系列答案
相关习题
（1）根据以上的数据建立一个2×2的列联表；
（2）若认为“性别与患色盲有关系”，则出错的概率会是多少
（本题可以参考两个分类变量x和y有关系的可信度表:）
性别与看营养说明列联表 单位: 名
(1)根据以上表格,写出 男 女 总计 看营养说明 50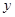 
80 不看营养说明 
20 30 总计 60 50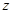 
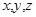的值.
(2)根据以上列联表，问有多大把握认为“性别与在购买食物时看营养说明”有关？
表示编号为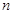
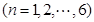的同学所得成绩，且前5位同学的成绩如下：
（1）求第6位同学的成绩编号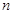
1
2
3
4
5
成绩
70
76
72
70
72
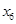，及这6位同学成绩的标准差
；
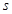（2）从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间（68，75）中的概率．
（1）求甲组同学植树棵树的平均数和方差；（参考公式: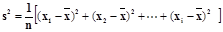
）
（2）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.
（1）求全班人数及分数在[80,90)之间的频数；
（2）估计该班的平均分数，并计算频率分布直方图中[80,90)间的矩形的高；
（3）若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[90,100]之间的概率.
标准煤)的几组对照数据：
(1)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程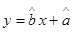
；
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(1)求出的线性回归方程，预测生产
l00吨甲产品的生产能耗比技改前降低多少吨标准煤?
（参考数值：3×2.5+4×3+5×4+6×4.5="66.5"
用最小二乘法求线性回归方程系数公式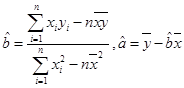
）.
从全校参加数学竞赛的学生的试卷中抽取一个样本，考察竞赛的成绩分布，将样本分成5组，绘成频率分布直方图，图中从左到右各小组的小长方形的高之比为1:3:6:4:2，最右边一组的频数是6，请结合直方图提供的信息，解答下列问题：
(1)样本的容量是多少？
(2)列出频率分布表；
(3)成绩落在哪个范围内的人数最多？并求出该小组的频数，频率；
(4)估计这次竞赛中，成绩高于60分的学生占总人数的百分比.
(1)请根据上表提供的数据， y关于x的线性回归方程x 3 4 5 6 y 2.5 3 4 4.5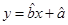 
；
(2)已知该厂技改前100吨甲产品生产能耗为90吨标准煤．试根据(1)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？（参考公式：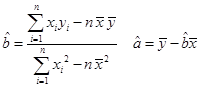
）
同步练习册答案
版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号
