
已知函数f(x)=lg(ax-bx)(a>1>b>0).
(1)求函数y=f(x)的定义域;
(2)在函数y=f(x)的图象上是否存在不同的两点,使过此两点的直线平行于x轴;
(3)当a、b满足什么关系时,f(x)在区间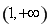 上恒取正值.
上恒取正值.
(1)(0,+∞)(2)不存在(3)a≥b+1
【解析】(1)由ax-bx>0,得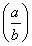 x>1,因为a>1>b>0,所以
x>1,因为a>1>b>0,所以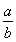 >1,所以x>0,即函数f(x)的定义域为(0,+∞).
>1,所以x>0,即函数f(x)的定义域为(0,+∞).
(2)设x1>x2>0,因为a>1>b>0,所以ax1>ax2,bx1<bx2,则-bx1>-bx2,所以ax1-bx1>ax2-bx2>0,于是lg(ax1-bx1)>lg(ax2-bx2),即f(x1)>f(x2),因此函数f(x)在区间(0,+∞)上是增函数.假设函数y=f(x)的图象上存在不同的两点A(x1,y1)、B(x2,y2),使得直线AB平行于x轴,即x1≠x2,y1=y2,这与f(x)是增函数矛盾.故函数y=f(x)的图象上不存在不同的两点,使过此两点的直线平行于x轴.
(3)由(2)知,f(x)在区间(1,+∞)上是增函数,所以当x∈(1,+∞)时,f(x)>f(1),故只需f(1)≥0,即lg(a-b)≥0,即a-b≥1,所以当a≥b+1时,f(x)在区间(1,+∞)上恒取正值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷(解析版) 题型:解答题
已知an=
(1)求数列{an}的前10项和S10;
(2)求数列{an}的前2k项和S2k.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第2课时练习卷(解析版) 题型:解答题
设等差数列{an}的前n项和为Sn,且S4=-62,S6=-75,求:
(1){an}的通项公式an及其前n项和Sn;
(2)|a1|+|a2|+|a3|+…+|a14|.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第1课时练习卷(解析版) 题型:解答题
已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第9课时练习卷(解析版) 题型:填空题
若函数f(x)=log2|ax-1|(a>0),当x≠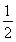 时,有f(x)=f(1-x),则a=________.
时,有f(x)=f(1-x),则a=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第9课时练习卷(解析版) 题型:填空题
(1)设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差是 ,则a=________;
,则a=________;
(2)若a=log0.40.3,b=log54,c=log20.8,用小于号“<”将a、b、c连结起来________;
(3)设f(x)=lg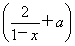 是奇函数,则使f(x)<0的x的取值范围是________;
是奇函数,则使f(x)<0的x的取值范围是________;
(4)已知函数f(x)=|log2x|,正实数m、n满足m<n且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m、n的值分别为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第8课时练习卷(解析版) 题型:填空题
设函数y=f(x)在(-∞,+∞)内有定义,对于给定的正数K,定义函数fK(x)=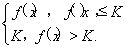 取函数f(x)=2-|x|.当K=
取函数f(x)=2-|x|.当K=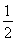 时,函数fK(x)的单调递增区间为________.
时,函数fK(x)的单调递增区间为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第5课时练习卷(解析版) 题型:填空题
已知直线y=a与函数f(x)=2x及g(x)=3·2x的图象分别相交于A、B两点,则A、B两点之间的距离为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com