
【题目】如图所示,直四棱柱![]() 的侧棱
的侧棱![]() 长为
长为![]() ,底面
,底面![]() 是边长
是边长![]()
![]() 的矩形,
的矩形,![]() 为
为![]() 的中点,
的中点,
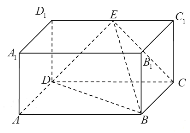
(1)求证:![]() 平面
平面![]() ,
,
(2)求异面直线![]() 与
与![]() 所成的角的大小(结果用反三角函数表示).
所成的角的大小(结果用反三角函数表示).
【答案】(1)见解析;(2)![]()
【解析】
(1)先证明EC⊥ED,再利用BC⊥平面CC1D1D,证明BC⊥DE,即可证明DE⊥平面EBC;
(2)取A1B1中点F,连接BF,DF,∠FBD即为所求异面直线的夹角(或其补角),确定△FBD为各边长,根据余弦定理可求∠FBD余弦值,从而求异面直线BD与EC所成的角的大小.
(1)证明:∵直四棱柱![]() 的侧棱
的侧棱![]() 长为
长为![]() ,
,
底面ABCD是边长AB=2a,BC=a的矩形,
![]() 为
为![]() 的中点,
的中点,
∴EC=ED=![]() a,CD=2a,
a,CD=2a,
∴EC⊥ED,
∵BC⊥平面![]() ,DE平面
,DE平面![]() ,
,
∴BC⊥DE,
∵BC∩EC=C
∴DE⊥平面EBC.
(2)取A1B1中点F,连接BF,DF,
易得EC∥FB,
∴∠FBD即为所求异面直线的夹角(或其补角),
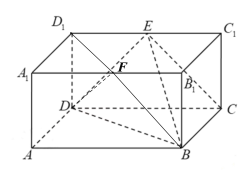
连接D1F,△DD1F为直角三角形,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
![]()
根据余弦定理,![]() ,
,
∴![]() ,
,
∴异面直线![]() 与
与![]() 所成的角的大小为
所成的角的大小为![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】已知定义在实数集![]() 上的偶函数
上的偶函数![]() 和奇函数
和奇函数![]() 满足
满足![]() .
.
(1)求![]() 与
与![]() 的解析式;
的解析式;
(2)求证:![]() 在区间
在区间![]() 上单调递增;并求
上单调递增;并求![]() 在区间
在区间![]() 的反函数;
的反函数;
(3)设![]() (其中
(其中![]() 为常数),若
为常数),若![]() 对于
对于![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名射击运动员在进行射击训练,已知甲命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,乙命中10环,9环,8环的概率分别是
,乙命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,任意两次射击相互独立.
,任意两次射击相互独立.
(1)求甲运动员两次射击命中环数之和恰好为18的概率;
(2)现在甲、乙两人进行射击比赛,每一轮比赛两人各射击1次,环数高于对方为胜,环数低于对方为负,环数相等为平局,规定连续胜利两轮的选手为最终的胜者,比赛结束,求恰好进行3轮射击后比赛结束的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年数学竞赛请自以为来自X星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题;然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答的题目则跳过(例如,他可以按照9,8,7,4,3,2,1,5,6,10的次序答题),这样所有的题目均有作答,设这位选手可能的答题次序有n种,则n的值为( )
A.512B.511C.1024D.1023
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆的一个顶点,△
是椭圆的一个顶点,△![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上一动点,求线段
上一动点,求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)过点![]() 分别作直线
分别作直线![]() ,
,![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为![]() ,
,![]() ,
,
且![]() ,探究:直线
,探究:直线![]() 是否过定点,并说明理由.
是否过定点,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使不等式f(x)≥2x-3对任意x∈R恒成立?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com