
【题目】已知圆C1的方程为x2+(y+1)2=4,圆C2的圆心坐标为(2,1).
(1)若圆C1与圆C2相交于A,B两点,且|AB|=![]() ,求点C1到直线AB的距离;
,求点C1到直线AB的距离;
(2)若圆C1与圆C2相内切,求圆C2的方程.
【答案】(1)![]() .(2)(x-2)2+(y-1)2=12+8
.(2)(x-2)2+(y-1)2=12+8![]() .
.
【解析】
(1) 知直线C1C2垂直平分公共弦AB.设直线AB与C1C2的交点为P,再解直角三角形得到
点C1到直线AB的距离.(2) 由两圆相内切得|C1C2|=|r1-r2|求出r2=2+2![]() ,即得圆
,即得圆
C2的方程.
(1)由题设,易知直线C1C2垂直平分公共弦AB.设直线AB与C1C2的交点为P,
则在Rt△APC1中,
∵|AC1|=2,|AP|=![]() |AB|=
|AB|=![]() ,
,
∴点C1到直线AB的距离为|C1P|=![]() .
.
(2)由题设得,圆C1的圆心为C1(0,-1),半径为r1=2.
设圆C2的半径为r2,则由两圆相内切得|C1C2|=|r1-r2|![]() =|2-r2|,
=|2-r2|,
解得r2=2+2![]() 或r2=2-2
或r2=2-2![]() (舍去).
(舍去).
故所求圆C2的方程为(x-2)2+(y-1)2=12+8![]() .
.


科目:高中数学 来源: 题型:
【题目】设f(x)=sinxcosx﹣cos2(x+ ![]() ).
).
(1)求f(x)的单调区间;
(2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,若f( ![]() )=0,a=1,求△ABC面积的最大值.
)=0,a=1,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
A.(0,﹣3)
B.(0,3)
C.(0,﹣2)
D.(0,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a,b的值.
(1)l1⊥l2,且l1过点(1,1);
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=![]() .
.
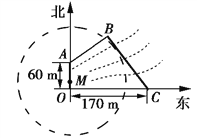
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩 ![]() 服从正态分布
服从正态分布 ![]() ,已知
,已知 ![]() ,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取
,若按成绩分层抽样的方式抽取100份试卷进行分析,则应从120分以上(包括120分)的试卷中抽取 ![]() 份;
份;
②已知命题 ![]() ,则
,则 ![]() :
: ![]() ;
;
③在 ![]() 上随机取一个数
上随机取一个数 ![]() ,能使函数
,能使函数 ![]() 在
在 ![]() 上有零点的概率为
上有零点的概率为 ![]() ;
;
④设 ![]() ,则“
,则“ ![]() ”是“
”是“ ![]() ”的充要条件.
”的充要条件.
其中真命题的序号为.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为( ![]() ,
, ![]() ),直线l的极坐标方程为ρcos(θ﹣
),直线l的极坐标方程为ρcos(θ﹣ ![]() )=a,且点A在直线l上,
)=a,且点A在直线l上,
(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为 ![]() (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com