
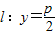 于点M,当|FD|=2时,∠AFD=60°.
于点M,当|FD|=2时,∠AFD=60°.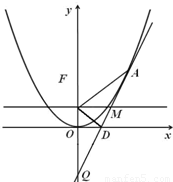
 ,则A处的切线方程为
,则A处的切线方程为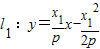 ,即可得到得D,Q的坐标,利用两点间的距离公式即可得到|FQ|=|AF|.由点A,Q,D的坐标可知:D为线段AQ的中点,利用等腰三角形的性质可得FD⊥AQ,可得|AF|,利用两点间的距离概率及点A满足抛物线的方程即可得出.
,即可得到得D,Q的坐标,利用两点间的距离公式即可得到|FQ|=|AF|.由点A,Q,D的坐标可知:D为线段AQ的中点,利用等腰三角形的性质可得FD⊥AQ,可得|AF|,利用两点间的距离概率及点A满足抛物线的方程即可得出.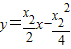 ,与切线l1的方程联立即可得到点P的坐标,同理求出点M,N的坐标.进而得到三角形PMN的面积
,与切线l1的方程联立即可得到点P的坐标,同理求出点M,N的坐标.进而得到三角形PMN的面积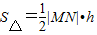 (h为点P到MN的距离),利用表达式及其导数即可得到最小值,即可得出x1的值.
(h为点P到MN的距离),利用表达式及其导数即可得到最小值,即可得出x1的值.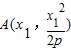 ,则A处的切线方程为
,则A处的切线方程为 ,
, ,
,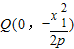
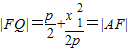 ;
;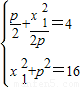
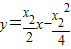
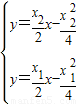 得到点P
得到点P ,联立
,联立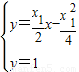 得到点M
得到点M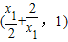 .
.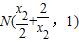 ,
,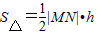 =
=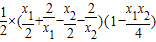 =
=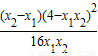 ①
①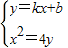 得到x2-4kx-4b=0,
得到x2-4kx-4b=0,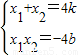 代入①得:S△=
代入①得:S△=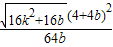 =
=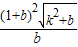 ,
,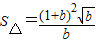 ②
②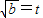 ,得
,得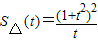 =
=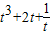 ,则
,则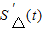 =
= ,
,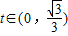 时,S(t)单调递减;当
时,S(t)单调递减;当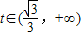 时,S(t)单调递增,
时,S(t)单调递增,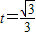 时,S取到最小值为
时,S取到最小值为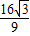 ,此时
,此时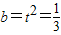 ,k=0,
,k=0,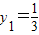 ,解得
,解得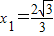 .
.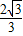 .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| AF |
| FB |
| AB |
| FQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
|
|
|
| ||
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com