
【题目】某企业打算处理一批产品,这些产品每箱100件,以箱为单位销售.已知这批产品中每箱出现的废品率只有![]() 或者
或者![]() 两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,有放回地随机从一箱中抽取2件产品进行检验.
①若此箱出现的废品率为![]() ,记抽到的废品数为
,记抽到的废品数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②若已发现在抽取检验的2件产品中,其中恰有一件是废品,判断是否可以购买.
【答案】(1) 在不开箱检验的情况下,可以购买. (2) ①分布列见解析,0.4 ②不可以购买
【解析】
(1)求出在不开箱检验的情况下,一箱产品中正品的价格期望值,即得解;(2)①![]() 的可能取值为0,1,2,再求出对应的概率,即得
的可能取值为0,1,2,再求出对应的概率,即得![]() 的分布列和数学期望;②一箱产品中,设正品的价格的期望值为
的分布列和数学期望;②一箱产品中,设正品的价格的期望值为![]() ,求出
,求出![]() 即得解.
即得解.
(1)在不开箱检验的情况下,一箱产品中正品的价格期望值为:
![]() ,
,
∴在不开箱检验的情况下,可以购买.
(2)①![]() 的可能取值为0,1,2,
的可能取值为0,1,2,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
| 0.64 | 0.32 | 0.04 |
![]() .
.
②设事件![]() :发现在抽取检验的2件产品中,其中恰有一件是废品,
:发现在抽取检验的2件产品中,其中恰有一件是废品,
则![]() ,
,
一箱产品中,设正品的价格的期望值为![]() ,则
,则![]() ,
,
事件![]() :抽取的废品率为
:抽取的废品率为![]() 的一箱,
的一箱,
![]() ,
,
事件![]() :抽取的废品率为
:抽取的废品率为![]() 的一箱,
的一箱,
则![]() ,
,
∴![]() ,
,
∴已发现在抽取检验的2件产品中,其中恰有一件是废品,不可以购买.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 恒过
恒过![]() 的一个焦点
的一个焦点![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)设![]() 为坐标原点,四边形
为坐标原点,四边形![]() 的顶点均在
的顶点均在![]() 上,
上,![]() 交于
交于![]() ,且
,且![]() ,若直线
,若直线![]() 的倾斜角的余弦值为
的倾斜角的余弦值为![]() ,求直线
,求直线![]() 与
与![]() 轴交点的坐标.
轴交点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第![]() 条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第
条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第![]() 条规定:对不礼让行人的驾驶员处以扣
条规定:对不礼让行人的驾驶员处以扣![]() 分,罚款
分,罚款![]() 元的处罚.下表是某市一主干路口监控设备所抓拍的
元的处罚.下表是某市一主干路口监控设备所抓拍的![]() 个月内驾驶员不“礼让斑马线”行为统计数据:
个月内驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
不“礼让斑马线”驾驶员人数 |
|
|
|
|
|
(1)请利用所给数据求不“礼让斑马线”驾驶员人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ,并预测该路口
,并预测该路口![]() 月份的不“礼让斑马线”驾驶员人数;
月份的不“礼让斑马线”驾驶员人数;
(2)若从表中![]() 月份和
月份和![]() 月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为
月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为![]() 的样本,再从这
的样本,再从这![]() 人中任选
人中任选![]() 人进行交规调查,求抽到的两人恰好来自同一月份的概率.
人进行交规调查,求抽到的两人恰好来自同一月份的概率.
参考公式: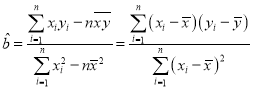 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红铃虫是棉花的主要害虫之一,能对农作物造成严重伤害,每只红铃虫的平均产卵数y和平均温度x有关,现收集了以往某地的7组数据,得到下面的散点图及一些统计量的值.(表中![]() )
)
平均温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 | ||
平均产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 | ||
|
|
|
|
| |||||
27.429 | 81.286 | 3.612 | 40.182 | 147.714 | |||||
(1)根据散点图判断,![]() 与
与![]() (其中
(其中![]() 自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
自然对数的底数)哪一个更适宜作为平均产卵数y关于平均温度x的回归方程类型?(给出判断即可,不必说明理由)并由判断结果及表中数据,求出y关于x的回归方程.(计算结果精确到小数点后第三位)
(2)根据以往统计,该地每年平均温度达到28℃以上时红铃虫会造成严重伤害,需要人工防治,其他情况均不需要人工防治记该地每年平均温度达到28℃以上的概率为![]() .
.
①记该地今后5年中,恰好需要3次人工防治的概率为![]() ,求
,求![]() 的最大值,并求出相应的概率p.
的最大值,并求出相应的概率p.
②当![]() 取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
取最大值时,记该地今后5年中,需要人工防治的次数为X,求X的数学期望和方差.
附:线性回归方程系数公式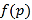 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在2016年的“减员增效”中对部分人员实行分流,规定分流人员第一年可以到原单位领取工资的100%,从第二年起,以后每年只能在原单位按上一年的![]() 领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得
领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得![]() 元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流后工资的收入每年
元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流后工资的收入每年![]() 元,分流后进入新经济实体,第
元,分流后进入新经济实体,第![]() 年的收入为
年的收入为![]() 元;
元;
(1)求![]() 的通项公式;
的通项公式;
(2)当![]() 时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
查看答案和解析>>
科目:高中数学 来源: 题型:
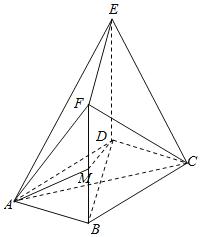
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.
(1)求BM的长;
(2)求二面角A﹣DM﹣B的余弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广东省2021年高考将实行“![]() ”模式,其最大特点就是取消文理科,除语文、数学、外语之外,从物理、历史这2科中自由选择一门科目;化学、生物、政治、地理这4科中自由选择两门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,从某学校高一年级的学生中随机抽取男生、女生个25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
”模式,其最大特点就是取消文理科,除语文、数学、外语之外,从物理、历史这2科中自由选择一门科目;化学、生物、政治、地理这4科中自由选择两门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,从某学校高一年级的学生中随机抽取男生、女生个25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
(1)请完成下面的![]() 列联表:
列联表:
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这50名学生中已经选取了男生3名,女生2名进行座谈,从这5人中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com