
【题目】已知长方形ABCD中,AB=1,AD=![]() 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
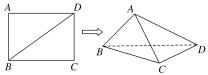
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
【答案】见解析
【解析】解:(1)若AB⊥CD,因为AB⊥AD,AD∩CD=D,
所以AB⊥平面ACD,所以AB⊥AC.
即AB2+a2=BC2,即12+a2=(![]() )2,所以a=1。
)2,所以a=1。
若AD⊥BC,因为AD⊥AB,
所以AD⊥平面ABC,所以AD⊥AC.
即AD2+a2=CD2,即(![]() )2+a2=12,
)2+a2=12,
所以a2=-1,无解.
故AD⊥BC不成立.
(2)要使四面体ABCD的体积最大,因为△BCD的面积为定值![]() ,
,
所以只需三棱锥ABCD的高最大即可,此时平面ABD⊥平面BCD,
过点A作AO⊥BD于点O,
则AO⊥平面BCD,
以O为坐标原点建立空间直角坐标系Oxyz(如图),
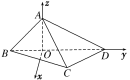
则易知A![]() ,C(
,C(![]() ,
,![]() ,0),D
,0),D![]() ,
,
显然,平面BCD的一个法向量为![]() =
=![]() 。
。
设平面ACD的法向量为n=(x,y,z).
因为![]() =
=![]() ,
,![]() =
=![]() ,
,
所以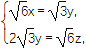 令y=
令y=![]() ,得n=(1,
,得n=(1,![]() ,2).
,2).
故二面角ACDB的余弦值为|cos〈![]() ,n〉|=
,n〉|=![]() =
=![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心
的圆心![]() 在
在![]() 轴上,半径为1,直线
轴上,半径为1,直线![]() 被圆
被圆![]() 所截的弦长为
所截的弦长为![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 的下方.
的下方.
(1)求圆![]() 的方程;
的方程;
(2)设![]() ,若圆
,若圆![]() 是
是![]() 的内切圆,求
的内切圆,求![]() 的面积
的面积![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)甲、乙两袋中各装有大小相同的小球![]() 个,其中甲袋中红色、黑色、白色小球的个数分别为
个,其中甲袋中红色、黑色、白色小球的个数分别为![]() 、
、![]() 、
、![]() ,乙袋中红色、黑色、白色小球的个数均为
,乙袋中红色、黑色、白色小球的个数均为![]() ,某人用左右手分别从甲、乙两袋中取球.
,某人用左右手分别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左右手依次各取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球的成功取法次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一个以![]() 、
、![]() 为半径的扇形池塘,在
为半径的扇形池塘,在![]() 、
、![]() 上分别取点
上分别取点![]() 、
、![]() ,作
,作![]() 、
、![]() 分别交弧
分别交弧![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,现用渔网沿着
,现用渔网沿着![]() 、
、![]() 、
、![]() 、
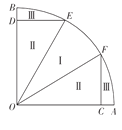
、![]() 将池塘分成如图所示的养殖区域.已知
将池塘分成如图所示的养殖区域.已知![]() ,
, ![]() ,
, ![]() (
(![]() ).
).
(1)若区域Ⅱ的总面积为![]() ,求
,求![]() 的值;
的值;
(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是30万元、40万元、20万元,试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCDA1B1C1D1中,AB=AA1=1,E为BC中点.
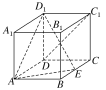
(1)求证:C1D⊥D1E;
(2)在棱AA1上是否存在一点M,使得BM∥平面AD1E?若存在,求![]() 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)若二面角B1AED1的大小为90°,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com