
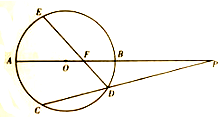
 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P.
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P.分析 (Ⅰ)若PD=8,CD=1,PO=9,利用割线定理求⊙O的半径;
(Ⅱ)连接OC、OE,先证明△PDF∽△POC,再利用割线定理,即可证得结论.
解答  (Ⅰ)解:∵PA交圆O于B,A,PC交圆O于C,D,
(Ⅰ)解:∵PA交圆O于B,A,PC交圆O于C,D,
∴PD•PC=PB•PA…(2分)
∴PD•PC=(PO-r)(PO-r)…(3分)
∴8×9=92-r2--------------(5分)
(Ⅱ)证明:连接EO CO
∵$\widehat{AE}$=$\widehat{AC}$,∴∠EOA=∠COA
∵∠EOC=2∠EDC,∠EOA=∠COA
∴∠EDC=∠AOC,∴∠COP=∠FDP…(7分)
∵∠P=∠P,∴△PDF~△POC---------------(9分)
∴PF•PO=PD•PC,
∵PD•PC=PB•PA,
∴PF•PO=PA•PB---------------(10分)
点评 本题考查的是圆周角定理,相似三角形的判定与性质及割线定理的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 定义域是[-1,1] | B. | f(x)是奇函数 | ||
| C. | 值域是[-tan1,tan1] | D. | 在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知在多面体SP-ABCD中,底面ABCD为矩形,AB=PC=1,AD=AS=2,且AS∥CP且AS⊥面ABCD,E为BC的中点.
已知在多面体SP-ABCD中,底面ABCD为矩形,AB=PC=1,AD=AS=2,且AS∥CP且AS⊥面ABCD,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知某几何体如图所示,若四边形ADMN为矩形,四边形ABCD为菱形,且∠DAB=60°,平面ADNM⊥平面ABCD,E为AB中点,AD=2,AM=1.
已知某几何体如图所示,若四边形ADMN为矩形,四边形ABCD为菱形,且∠DAB=60°,平面ADNM⊥平面ABCD,E为AB中点,AD=2,AM=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{3}$) | B. | (-∞,0] | C. | (-∞,1) | D. | (-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com